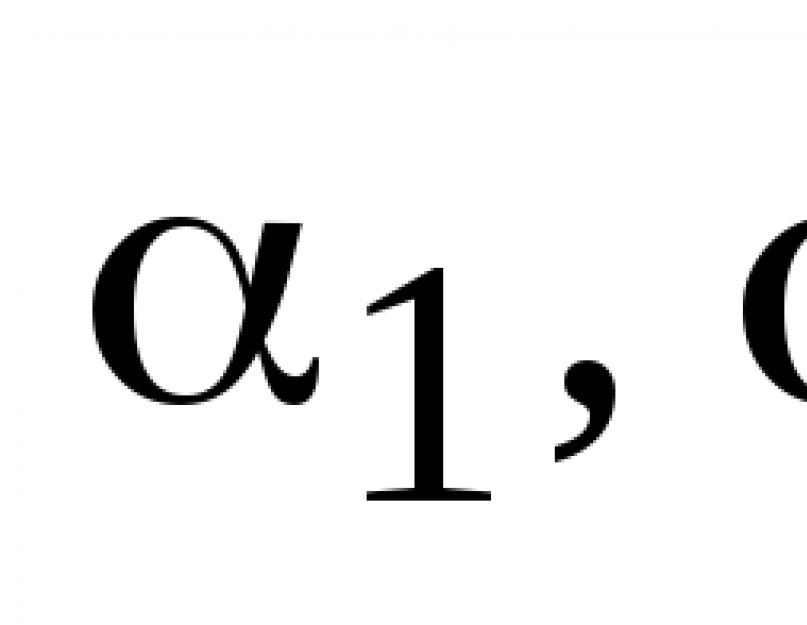Prelegeri de algebră și geometrie. Semestrul 1

Cursul 9. Bazele spațiului vectorial.

Pe termen scurt: sistem vectorial, combinație liniară a sistemului vectorial, coeficienți de combinație liniară a sistemului vectorial, baza pe o dreaptă, aria și spațiul, dimensiunile spațiilor vectoriale pe o dreaptă, aria și în spațiu, descompunerea vectorului conform baza, coordonatele vectorului conform bazei, teorema despre gelozie doi vectori, operatii liniare pe vectori in notatie de coordonate, triplu ortonormal al vectorilor, triplu dreapta si stanga al vectorilor, baza ortonormala, teorema principala a algebrei vectoriale.

Capitolul 9. Baza spațiului vectorial și descompunerea vectorului din spatele bazei.

clauza 1. Baza este pe o linie dreaptă, pe o suprafață plană și în spațiu.

Viznachennya. Oricum, vectorii nesfârșiti sunt numiți un sistem de vectori.

Viznachennya. Viraz, de
se numește combinație liniară a unui sistem vectorial
, și numerele
se numesc coeficienți ai combinației liniare.

Fie L, P și S – drept, aria și spațiul punctului sunt paralele și
. Todi
- Spațiile vectoriale ale vectorilor ca tăieturi directe pe dreapta L, pe planul P și în spațiul S sunt consistente.

numit vector diferit de zero
, apoi. fie orice vector coliniar diferit de zero L:
і
.

Atribuit la bază
:
- Baza
.

Viznachennya. Baza spațiului vectorial
se numește dacă o pereche de vectori necoliniari în spațiu este ordonată
.

, de
,
- Baza
.

Viznachennya. Baza spațiului vectorial
se numește atunci când trei vectori necoplanari sunt ordonați (pentru a nu se afla în același plan) în spațiu
.

- Baza
.

Respect. Baza spațiului vectorial nu poate înlocui vectorul zero: în spațiu
în culise, în spațiul deschis
doi vectori vor fi coliniari, ca și cum unul dintre ei ar fi zero, în spațiu
trei vectori vor fi coplanari, deci se află în același plan, ca și cum unul dintre cei trei vectori ar fi zero.

clauza 2. Așezarea vectorului pe baza.

Viznachennya. Să mergem – un vector suficient,
- Un destul de sistem de vectori. Cum se termină gelozia

pare un vector reprezentările par a fi o combinație liniară de sisteme vectoriale. Este dat un sistem de vectori
є baza spațiului vectorial, atunci egalitatea (1) se numește descompunerea vectorului pe bază
. Coeficienți de combinație liniară
se numesc astfel coordonatele vectorului la bază
.

Teorema. (Despre descompunerea vectorilor din spatele bazei.)

Orice vector al unui spațiu vectorial poate fi împărțit în baza sa într-un singur mod.

Terminat. 1) Fie L să fie mulțumit cu linia dreaptă (sau cu totul)
- Baza
. Să luăm un vector foarte frumos
. Deci cât de jigniți sunt vectorii і Coliniar unul și același și drept L, atunci
. Teorema vitezei despre coliniaritatea a doi vectori. Deci iac
, atunci va exista un astfel de număr
, ce
Și astfel noi înșine am descompus vectorul pe bază
spațiu vectorial
.

Acum vom demonstra unitatea unui astfel de aspect. Inacceptabil. Să avem doi vectori pliați pe bază
spațiu vectorial
:

і
, de
. Todi
iar legea vikoristă a distributivității este respinsă:

Deci iac
, apoi cu râvna rămasă curge că
, Ch.t.d.

2) Lăsați-l acum să fie suficient de plat
- Baza
. Să mergem
vector suplimentar al zonei. Adăugăm toți cei trei vectori la orice punct al aceluiași plan. Să rămânem 4 drepte. Să mergem drept , pe care se află vectorul direct
, pe care se află vectorul . Până la sfârșitul vectorului trage direct paralel cu vectorul este direct paralel cu vectorul . Cele 4 linii drepte atârnă în paralelograme. mai jos fig. 3. Urmând regula paralelogramului
, і
,
,
- Baza ,
- Baza
.

Acum, după ce am terminat deja prima parte a acestei dovezi, există astfel de numere
, ce

і
. Stelele sunt clare:

iar posibilitatea de a pune bazele a fost realizată.

Acum vom demonstra unitatea descompunerii după bază. Inacceptabil. Să avem doi vectori pliați pe bază
spațiu vectorial
:
і
. Gelozia este demontabilă

Urmează stele
. Yakshcho
, Acea
, Și de când
, Acea
și coeficienții nivelului stabilit:
,
. Sa mergem acum
. Todi
, de
. Urmând teorema despre coliniaritatea a doi vectori, rezultă că
. Au apărut teoreme uluitoare. Otje,
і
, Ch.t.d.

3) Lasă-o
- Baza
și dă-mi drumul
frumos vector. Să petrecem ceva timp așa.

Includem toți cei trei vectori de bază
ta vector De la un punct vor fi 6 planuri: planul în care se află vectorii de bază
, zona
acea zonă
; distanța până la capătul vectorului Să desenăm trei planuri în paralel, creând cu atenție trei planuri. Există 6 avioane atârnând paralelipiped:

Regula de pliere a vectorilor implică gelozia:

. (1)

În fiecare zi
. Pe baza teoremei despre coliniaritatea a doi vectori, rezultă că numărul principal
, şi ce dacă
. De asemenea,
і
, de
. Acum, înlocuind egalitățile (1), putem elimina:

iar posibilitatea de a pune bazele a fost realizată.

Să demonstrăm unitatea unui astfel de aspect. Inacceptabil. Să avem doi vectori pliați pe bază
:

eu. Todi

Dragă, ce se află în spatele vectorului creierului
necoplanare, deci miros perechi necoliniar.

Există două scenarii posibile:
sau
.

a) Dă-i drumul
, Todi cu zel (3) țipă:

. (4)

Cu gelozia (4) strălucește ca un vector descompuse după bază
, apoi. vector se află lângă pătratul vectorial
și, de asemenea, vectori
coplanar, care supraalimentează mintea.

b) Pierderea căderii
, apoi.
. Todi cu egalitate (3) poate fi eliminat sau

Deci iac
- baza spatiului vectorilor se afla in plan, si am adus deja unitatea descompunerii dupa baza vectorilor ariei, apoi din egalitatea (5) rezulta ca
і
, Ch.t.d.

Teorema a fost demonstrată.

Ancheta.

1) Există o relație reciproc neechivocă între vectorii anonimi din spațiul vectorial
și fără numere active R.

2) Există o corespondență reciproc neechivocă între vectorii anonimi din spațiul vectorial
și un pătrat cartezian

3) Există o corespondență reciproc neechivocă între vectorii anonimi din spațiul vectorial
și un cub cartezian
multiplicitățile numerelor reale R.

Terminat. Am ajuns la al treilea punct. Primele două sunt tratate într-un mod similar.

Selectați și fixați în spațiu
ce bază
iar afișajul este controlat
urmând următoarea regulă:

tobto. Vectorul de piele este setat la tipul setului de coordonate ordonat.

Deoarece, cu o bază fixă, vectorul conține un singur set de coordonate, atunci aspectul, care este specificat de regula (6), este eficient în imagini.

Dovada teoremei arată că diferiți vectori au coordonate diferite bazate pe aceeași bază. Afișajul (6) înseamnă că nu există efect.

Să mergem
Mai multă ordonare a apelării numerelor active.

Să aruncăm o privire asupra vectorului
. Acest vector are coordonate
. Ei bine, imaginea (6) este sur'ecce.

Imaginea este atât inactivă, cât și suractivă și ineficientă. reciproc fără ambiguitate etc.

Ancheta a fost finalizată.

Teorema. (Despre egalitatea a doi vectori.)

Doi vectori sunt egali dacă coordonatele lor sunt egale cu aceeași bază.

Dovada reiese imediat din cercetarea prealabilă.

clauza 3. Dimensiunea spațiului vectorial.

Viznachennya. Numărul de vectori din baza unui spațiu vectorial se numește dimensiunea acestuia.

Desemnat:
- Mărimea spațiului vectorial V.

Astfel, asemănând cu aceasta și cu valorile anterioare, putem spune:

1)
- Spațiul vectorial al vectorilor linii L.

- Baza
,
,
,
- Vector de aspect
pe bază
,
– coordonata vectoriala la bază
.

2)
- Spațiul vectorial al vectorilor zonei R.

- Baza
,
,
,
- Vector de aspect
pe bază
,
– coordonate vectoriale la bază
.

3)
– spațiu vectorial al vectorilor în punctul spațial S.

- Baza
,
,
- Vector de aspect
pe bază
,
– coordonate vectoriale la bază
.

Respect. Yakshcho
, Acea
și puteți selecta baza
spaţiu
şi ce dacă
- Baza
і
- Baza
. Todi
, і
, .

În acest fel, orice vector al dreptei L, ariei P sau spațiului S poate fi împărțit în funcție de bază
:

Programare. În virtutea teoremei despre egalitatea vectorilor, putem identifica orice vector dintr-un trio ordonat de numere reale și putem scrie:

Acest lucru poate fi mai puțin important în acest caz, dacă baza
fixari si nu exista pericolul de a se confunda.

Viznachennya. Scrierea unui vector sub forma unui trio ordonat de numere reale se numește formă de coordonate scrierea unui vector:
.

clauza 4. Operații liniare cu vectori sub formă de notație de coordonate.

Să mergem
– baza spatiului
і
– doi vectori suplimentari. Să mergem
і
– înregistrarea acestor vectori în formă de coordonate. Haide, mergi înainte,
- Un număr destul de eficient. Aceste nume au aceeași teoremă.

Teorema. (Despre operațiile liniare cu vectori sub formă de coordonate.)

2)
.

Cu alte cuvinte, pentru a adăuga doi vectori, trebuie să adăugați coordonatele lor, iar pentru a înmulți un vector cu un număr, trebuie să înmulțiți coordonatele unui vector dat cu un număr dat.

Terminat. Urmând teorema mentală, se scad axiomele vikoriste ale spațiului vectorial, care stau la baza operațiilor de pliere a vectorilor și de înmulțire a unui vector cu un număr:

Steaua țipă.

Același lucru este valabil și pentru gelozie.

Teorema a fost demonstrată.

clauza 5. Vectori ortogonali. Baza ortonormala.

Viznachennya. Doi vectori sunt numiți ortogonali, deoarece calea dintre ei este similară cu calea directă.
.

Desemnat:
- Vectori і ortogonală

Viznachennya. Trei vectori
se numește ortogonal deoarece vectorii sunt ortogonali unul față de celălalt, atunci.
,
.

Viznachennya. Trei vectori
se numește ortonormal pentru că este ortogonal și până când toți vectorii au unități:
.

Respect. Valoarea rezultă că triplul vectorilor este ortogonal și, prin urmare, ortonormal și necoplanar.

Viznachennya. Este ordonat un trio necoplanar de vectori
, plasat în același punct, se numește dreapta (orientată spre dreapta), deoarece provine de la sfârșitul celui de-al treilea vector la zona în care se află primii doi vectori і , cea mai scurtă rotație a primului vector altcuiva apare vizavi de săgeata aniversară. În celălalt caz, cei trei vectori se numesc stânga (orientați la stânga).

Aici, în Fig. 6, sunt prezentați cei trei vectori din dreapta
. Următoarea figură 7 prezintă cei trei vectori din stânga
:

Viznachennya. Bază
spațiu vectorial
se numeste ortonormalizare, deoarece
Trioul de vectori este ortonormal.

Programare. Avem o bază ortonormală corectă.
div. atacându-i pe cei mici.

Linearitatea și liniaritatea vectorilor.
Baze vectoriale. Sistemul de coordonate atenian

Vor fi multe bomboane de ciocolată în clasă, iar balsamul de piele va primi astăzi un cuplu de lemn dulce - geometrie analitică cu algebră liniară. În acest articol, două secțiuni ale matematicii majore vor fi distruse și ne vom întreba cum trăiesc într-o singură ardere. Ia o pauză și joacă „Twix”! ...mlynets, bine, și nіsenіtnitsa superechok. Dacă vreau, nu voi renunța, voi începe cu o atitudine pozitivă.

Localizarea liniară a vectorilor, independența liniară a vectorilor, baza de vectori Cu toate acestea, termenii pot avea nu numai o interpretare geometrică, ci, mai presus de toate, un sens algebric. După ce am înțeles „vectorul” însuși din perspectiva algebrei liniare, nu este în niciun caz același vector „primar” pe care îl putem reprezenta pe un plan sau în spațiu. Nu trebuie să cauți departe pentru dovezi, doar încearcă să pictezi un vector al întinderii penta-lumi. . Sau stai, pentru care am fost la Gismeteo: - temperatura si presiunea atmosferica sunt consistente. Fundul, desigur, este incorect din punctul de vedere al autorităților din spațiul vectorial, dar nimeni nu se deranjează să formalizeze acești parametri cu un vector. Dihana toamnei.

Nu, nu intenționez să vă atrag cu teoria, spațiile vectoriale liniare, scopul este ca a intelege sensul teoremei. Termeni noi (liniaritate, independență, combinație liniară, bază etc.) sunt aplicați tuturor vectorilor din punctul de vedere al algebrei, dar aplicațiile vor fi geometrice. În acest fel, totul este simplu, accesibil și în persoană. Pe lângă sarcina de geometrie analitică, ne vom uita la tipurile de sarcini ale algebrei. Pentru a stăpâni materialul, este important să vă familiarizați cu lecțiile Vectori pentru manechineі Cum calculezi valoarea?

Linearitatea și independența vectorilor de zonă.
Baza planului și a sistemului de coordonate afine

Să aruncăm o privire la suprafața mesei pentru calculator (doar o masă, noptiere, noptiere, suporturi, orice ți se potrivește). Zavodannya va rămâne în ofensivă:

1) Planul de bază al vibrațiilor. În linii mari, coloana are lungime și lățime, așa că s-a înțeles intuitiv că sunt necesari doi vectori pentru a forma o bază. Un vector nu este suficient, trei vectori sunt o risipă.

2) Bazat pe baza selectată inserarea sistemului de coordonate(grilă de coordonate) pentru a atribui coordonate tuturor obiectelor de pe tabel.

Nu fi surprins, explicația va fi pe degete imediat. Mai mult, pe a ta. Fii amabil, loc degetul vulgar al mâinii stângi până la marginea camerei, astfel încât să te minunezi de monitor. Acesta va fi un vector. Acum loc degetul mic al mâinii drepte pe marginea mesei exact așa - astfel încât să fie direct pe ecranul monitorului. Acesta va fi un vector. Zâmbește, arăți minunat! Ce poți spune despre vectori? vectori Dani coliniar, care înseamnă liniar apar unul dupa altul:
, ei bine, de fapt: , de – număr deyake, vydmіnne vіd zero.

Puteți vedea o imagine a acestei acțiuni în lecție Vectori pentru manechine Unde am explicat regula înmulțirii unui vector cu un număr.

Cum vor așeza degetele tale baza pe suprafața mesei computerului? Evident, nu. Vectorii coliniari vor crește prețul ici și acolo singur drept, iar suprafața este egală cu lățimea.

Aceștia sunt vectorii numiți mincind liniar.

Dovidka: Cuvintele „liniar”, „liniar” înseamnă că în ecuațiile matematice nu există pătrate, cuburi, alți pași, logaritmi, sinusuri etc. Numai expresii și plasamente liniare (etapa I).

Două planuri vectoriale depozite liniare Aceasta și numai aceasta, dacă sunt coliniare.

Împășește-ți degetele pe masă, astfel încât între ele să existe vreo diferență între 0 și 180 de grade. Două planuri vectorialeliniar Nu depuneri în acest sau acel caz, deoarece duhoarea nu este coliniară. Ei bine, baza a fost eliminată. Nu este nevoie să vă faceți griji cu privire la „tunsul” bazei Wijshov-ului cu vectori neperpendiculari ai diferitelor dovzhin. Este important pentru noi că în acest scop nu există doar 90 de grade și nu doar vectori unici, egali.

Tot ceea ce vector zonă într-un singur rang descompus conform bazei:
, numere de-operaționale. Denumiți numerele coordonate vectoriale pe ce bază.

Deci se pare că vectorvederi de la privitor combinație liniară vectori de bază. Așa numesc ei viraz vector de desfășurarepe bază sau combinație liniară vectori de bază.

De exemplu, putem spune că vectorul de descompunere în spatele bazei ortonormale a planului, și putem spune că reprezentările au aspectul unei combinații liniare de vectori.

Lasă-mă să formulez valoare la bază oficial: Baza zonei o pereche de vectori liniar independenți (necoliniari) se numește, , când fie ce-o fi Vectorul zonă este o combinație liniară de vectori de bază.

Momentul real de semnificație este faptul că vectorii luați în ordinea cântării. Basisi – acestea sunt două baze absolut diferite! Se pare că nu poți înlocui degetul mic de la mâna stângă cu degetul mic de la mâna dreaptă.

Am aranjat baza, dar nu este suficient să setați o grilă de coordonate și să atribuiți coordonate fiecărui obiect de pe tabelul computerului dvs. De ce nu suficient? Vectorii sunt liberi și rătăcesc pe toată suprafața. Deci, cum putem da coordonatele acestor mici puncte brute de pe masă pe care le-am pierdut după un weekend agitat? Punct de referință necesar. Și un astfel de punct de referință este un punct cunoscut de toată lumea - începutul coordonatelor. Să ne uităm la sistemul de coordonate:

Voi începe cu organizarea „școală”. Deja la lecția introductivă Vectori pentru manechine Am văzut diferențele dintre sistemul de coordonate rectiliniu și baza ortonormală. Imagine standard axului:

Când vorbim despre sistem de coordonate rectiliniu, atunci cel mai adesea sunt vizibile coordonatele, axele de coordonate și scara de-a lungul axelor. Încercați să introduceți „sistem de coordonate direct” în motorul de căutare și veți vedea că veți învăța multe despre axele de coordonate pe care le cunoașteți din clasa a 5-a-6 și cum să plasați punctele pe un avion.

Pe de altă parte, rezultă că un sistem de coordonate rectiliniu poate fi definit în întregime printr-o bază ortonormală. Și probabil că este adevărat. Formula ar trebui să sune așa:

cob de coordonate, і ortonormalitati pune bazele Sistem de coordonate plan rectiliniu cartezian . Este un sistem de coordonate rectiliniu categoric este reprezentată printr-un singur punct și doi vectori unici ortogonali. Vedeți acest lucru în scaunul în sine, așa cum sunt obișnuit - în lucrările geometrice, atât vectorii, cât și axele de coordonate sunt adesea (dar nu întotdeauna) desenate.

Cred că toată lumea și-a dat seama că dincolo de punct (coordonate) există o bază ortonormală FI PUNCTUL AVIONULUI SI FI VECTORUL AVIONULUI pot fi atribuite coordonate. Figurat vorbind, „totul de pe pătrat poate fi numerotat”.

Se presupune că vectorii de coordonate sunt unici? Nu, pot plăti destul de mulți bani. Să ne uităm la punctul și doi vectori ortogonali cu o valoare suficient de diferită de zero:

O astfel de bază se numește ortogonală. Un set de coordonate cu vectori definește o grilă de coordonate și orice punct din plan sau vector își urmărește coordonatele pe această bază. De exemplu, sau... Inconsistența evidentă constă în faptul că vectorii de coordonate la zagalny vipadku Există diferite dovzhins, subîmpărțite într-unul singur. De îndată ce unitățile cresc în dimensiune, atunci apare o bază ortonormală primară.

! Notă : în baza ortogonală și, de asemenea, mai jos în bazele afine, se iau în considerare aria și spațiul unuia de-a lungul axelor UMOVIMI. De exemplu, într-o unitate de-a lungul axei absciselor există 4 cm, într-o unitate de-a lungul axei ordonatelor există 2 cm. Aceste informații sunt suficiente pentru, dacă este necesar, să traducă coordonatele „non-standard” în „centimetrii noștri inițiali”.

Și încă un aliment, așa cum a fost deja dat adevărul - care este legătura dintre vectorii de bază care pot fi egali cu 90 de grade? Nu! Cum se determină semnificația, vectorii de bază ai vinovăției mai puțin necoliniară. Aparent, poate fi oriunde între 0 și 180 de grade.

Punctul planului se numește cob de coordonate, і necoliniare vectori, , a stabilit sistemul de coordonate afín al planului :

Uneori se numește acest sistem de coordonate oblic sistem. Ca imaginea capului de pe scaun a punctului și vectorului:

După cum vă puteți imagina, sistemul de coordonate afine este și mai puțin manual, nu funcționează cu formule de dublare a vectorilor și tăierilor, așa cum am văzut într-o altă parte a lecției. Vectori pentru manechine, formule bogat delicioase asociate cu crearea scalară a vectorilor. Apoi, există următoarele reguli pentru adăugarea vectorilor și înmulțirea unui vector cu un număr, formule pentru subsecțiunea din această relație, precum și acțiuni ale tipului de sarcină pe care o vom analiza pe scurt.

Și conceptul este de așa natură încât cel mai convenabil mod de a descrie sistemul de coordonate afine este sistemul rectiliniu cartezian. De aceea, draga mea, cel mai adesea trebuie să studiez. ... În acest caz, totul în viața cuiva este clar - se bazează pe situația în care râul însuși este deformat (sau altele, de exemplu, polar) sistem de coordonate. Humanoizii se pot bucura de astfel de sisteme =)

Să trecem la partea practică. Toate informațiile oferite în această lecție sunt corecte atât în ​​sistemul de coordonate rectiliniu, cât și în forma afonică. Nu este nimic complicat aici, tot materialul este accesibil unui student.

Cum se determină coliniaritatea vectorilor de zonă?

Bogați tipic. Pentru a avea doi vectori și plane Dacă sunt coliniare, este necesar și suficient ca coordonatele lor să fie proporționale. De fapt, nu există nicio detaliere coordonată a relației evidente.

fundul 1

a) Verificați dacă vectorii sunt coliniari .
b) Chi stabilește vectorii de bază ?

Decizie:
a) Este clar ce înseamnă pentru vectori coeficient de proporționalitate, astfel încât egalitățile sunt egale:

Să vorbim cu siguranță despre versiunea „la modă” a regulii stabilite, care în general se aplică în practică. Ideea este de a rectifica imediat proporția și de a te întreba dacă este adevărată:

Adunăm proporția din liniile coordonatelor corespunzătoare ale vectorilor:

Scurt:
, astfel, coordonatele externe sunt proporționale, prin urmare,

Instalarea ar putea fi pliată și pliată, deci aceeași opțiune:

Pentru autoverificare, le puteți verifica pe acelea care vectorii coliniari exprimă liniar unu prin unu. În cazul căruia se profilează locul geloziei . Dreptatea lor poate fi ușor verificată prin acțiuni elementare cu vectori:

b) Doi vectori de arie formează o bază deoarece sunt coliniari (liniar independenți). Monitorizăm coliniaritatea vectorilor . Stivuim sistemul:

Din prima, iese ecuația, care, din cealaltă, iese rivalitatea, care, apoi, sistemul este absurd(Nu există soluție). Astfel, coordonatele reale ale vectorilor nu sunt proporționale.

Visnovok: vectorii sunt independenți liniar și creează o bază.

O versiune simplificată a soluției arată astfel:

Adunăm proporția din coordonatele corespunzătoare ale vectorilor :
Prin urmare, acești vectori sunt independenți liniar și creează o bază.

Asigurați-vă că această opțiune este respinsă de evaluatori, altfel problema va apărea dacă coordonatele ajung la zero. Axa este astfel: . Sau cam asa: . Sau cam asa: . Cum lucrăm prin proporție? (Ca să fiu sincer, nu poți împărți la zero). Tocmai din acest motiv, am numit soluția simplificată „foppish”.

Subiect: a), b) afirmă.

Un mic exemplu creativ pentru creativitate independentă:

fundul 2

Pentru orice valoare a parametrului vectorial vor exista coliniarități?

În soluție, parametrul se găsește prin proporție.

Se bazează pe o metodă rafinată de algebră pentru verificarea colinearității vectorilor.Ne sistematizăm cunoștințele și adăugăm al cincilea punct:

Pentru doi vectori de suprafață, etapele echivalente ale călirii:

2) vectorii definesc baza;
3) vectorii nu sunt coliniari;

+ 5) primar, adunarea coordonatelor acestor vectori, subordonați zero.

Aparent, duritate echivalentă a piciorului și a patului:
1) vectori liniari;
2) vectorii nu sunt egali cu baza;
3) vectorii sunt coliniari;
4) vectorii pot fi exprimați liniar unu prin unu;
+ 5) primar, adunare din coordonatele acestor vectori, egal cu zero.

Sunt deja convins că până acum ați înțeles deja toți termenii și afirmațiile care au devenit familiare.

Să aruncăm o privire la noul punct al cincilea al raportului: doi vectori de zonă Metode coliniare și numai cele, dacă originea, sunt pliate din coordonatele acestor vectori, relativ la zero:. Pentru a completa aceste semne, desigur, trebuie să rețineți cunosc și învingători.

Virishimo Butt 1 într-un alt fel:

a) Covariata adunării coordonatelor vectorilor este calculabilă :
, atunci, vectorii sunt coliniari.

b) Doi vectori de arie formează o bază deoarece sunt coliniari (liniar independenți). Covariata coordonatelor vectoriale este calculabilă :
, De asemenea, vectorii sunt independenți liniar și creează o bază.

Subiect: a), b) afirmă.

Arată mult mai compact și mai frumos, cu proporții mai puține.

Cu ajutorul materialului luat în considerare se poate stabili coliniaritatea vectorilor, și să se stabilească paralelismul secțiunilor și liniilor drepte. Să ne uităm la câteva comenzi cu figuri geometrice specifice.

fundul 3

Având în vedere vârfurile Chotirikutnikului. Să știu că Chotirikutnik este un paralelogram.

Terminat: Nu va fi nevoie de un fotoliu în problemă, restul soluției va fi pur analitică. Putem ghici semnificația paralelogramului:
Paralelogram Se numește chotirikutnik, ale cărui laturi procumbe sunt paralele la perechi.

În acest fel, este necesar să se transmită:
1) paralelismul laturilor proximale;
2) paralelismul laturilor opuse.

Convingător:

1) Cunoaștem vectorii:

2) Cunoaștem vectorii:

Viyshov este același vector („conform școlii” - vectori egali). Coliniaritatea este deja evidentă, dar este mai bine să oficializați decizia într-o manieră clară, bine aranjată. Covariata adunării coordonatelor vectorilor este calculabilă:
, De asemenea, vectorii sunt coliniari și .

Visnovok: Laturile opuse ale mesteacănului sunt paralele în perechi, prin urmare, în spatele semnificațiilor se află un paralelogram. Ce trebuia adus în discuție.

Cifre mai bune și diferite:

fundul 4

Având în vedere vârfurile Chotirikutnikului. Anunțați-ne că chotirikutnik este un trapez.

Pentru a formula mai bine dovada, este imperativ să obțineți un trapez mare sau doar să stați și să ghiciți cum arată.

Acesta este scopul deciziei independente. Mai presus de toate, soluția este similară cu lecția.

Și acum a sosit momentul să trecem încet din pătrat în spațiul deschis:

Cum se determină coliniaritatea vectorilor în spațiu?

Regula este foarte asemănătoare. Pentru ca doi vectori spațiali să fie coliniari, este necesar și suficient ca coordonatele lor relative să fie proporționale.

fundul 5

Să știți că vectorii coliniari vor fi disponibili în spațiu:

A);
b)
V)

Decizie:
a) Să verificăm care este coeficientul de proporționalitate pentru coordonatele vectoriale corespunzătoare:

Sistemul nu are soluție, deoarece vectorii nu sunt coliniari.

„Sproshchenka” este oficializată prin inversarea proporțiilor. In aceasta sectiune:
– coordonatele nu sunt proporționale, iar vectorii nu sunt coliniari.

Subiect: vectorii nu sunt coliniari.

b-c) Acestea sunt punctele de decizie independentă. Încercați să o proiectați în două moduri diferite.

Există o metodă de verificare a vectorilor spațiali pentru coliniaritate și printr-o origine de ordinul trei, având în vedere metoda prezentată în articol Vectori tvr vector.

Similar cu o tăietură plată, uneltele luate în considerare pot fi stivuite prin urmărirea paralelismului tăierilor spațiale și liniilor drepte.

Vă rugăm să mai aveți o secțiune:

Linearitatea și independența vectorilor în spațiul trivial.
Bază extinsă și sistem de coordonate afine

Multe dintre modelele pe care le-am văzut pe câmpie vor fi corecte în spațiul deschis. Am încercat să minimizez abstractul din teorie, fragmentele din partea stângă a informației au fost deja dezvăluite. Tim, nu mai puțin, vă recomand să citiți cu atenție partea introductivă, pe măsură ce sunt introduși termeni și concepte noi.

Acum, în locul zonei biroului computerului, există un spațiu tridimensional. Să creăm această bază de acum înainte. Fie că suntem în interior sau pe stradă, nu vom putea niciodată să întâlnim cele trei lumi ale lățimii, adâncimii și înălțimii. Prin urmare, pentru a forma o bază, sunt necesari trei vectori spațiali. Unul sau doi vectori nu sunt de ajuns, sferturile sunt grozave.

Framant din nou pe degete. Fii amabil, ridică mâna și deschide-ți diferitele părți degetul mare, impresionant și mijlociu. Vor fi vectori, vor apărea mirosuri pe părți diferite, vor exista diferențe diferite între ele și vor exista mirosuri diferite între ele. Văd, baza banalei întinderi este gata! Înainte de a vorbi, nu este nevoie să demonstrezi așa ceva în conturile tale, doar nu-ți învârti degetele și nu vei ajunge nicăieri =)

Să punem alimente mai importante în viitor, fie că este vorba de trei vectori care creează baza spațiului trivial? Fiți amabil, apăsați ferm trei degete pe partea laterală a mesei computerului. Ce s-a întâmplat? Trei vectori s-au mișcat într-un singur plan și, aproximativ vorbind, cunoșteam una dintre lumi dispărute - înălțimea. Astfel de vectori coplanareȘi este complet evident că baza spațiului trivial nu poate fi creată.

Trebuie remarcat faptul că vectorii coplanari nu se află în același plan, dar pot fi localizați în planuri paralele (lucrați doar cu degetele, deci este mai dificil pentru Salvador Dali =)).

Viznachennya: se numesc vectorii coplanare Deoarece există o câmpie, care este paralelă cu mirosul. Aici este logic să adăugați că dacă nu există o astfel de zonă, atunci vectorii nu vor fi coplanari.

Trei vectori coplanari sunt întotdeauna liniari apoi sunt exprimate liniar unu prin unu. Pentru simplitate, este din nou acceptabil ca duhoarea să se afle în aceeași zonă. În primul rând, vectorii care nu sunt doar coplanari pot fi și coliniari, astfel încât orice vector poate fi exprimat prin orice vector. Într-un alt caz, deoarece, de exemplu, vectorii nu sunt coliniari, atunci al treilea vector este exprimat prin ei într-o singură formă: (De ce este ușor de ghicit din materialele din secțiunea frontală).

Corect este acel punct de cotitură: trei vectori necoplanari sunt întotdeauna liniar independenți, pentru ca ei să nu se exprime unul câte unul. Și, evident, doar astfel de vectori pot crea baza unui spațiu trivial.

Viznachennya: Baza spațiului trivial se numește un trio de vectori liniar independenți (necoplanari), luate din ordinul cântului oricare ar fi vectorul spațiului într-un singur rang descompuse pe o bază dată, unde coordonatele vectorului în această bază

Bănuiesc, puteți spune și că vectorul reprezentărilor din vedere combinație liniară vectori de bază.

Conceptul de sistem de coordonate este introdus în același mod ca și pentru o diagramă plată, un punct sau trei vectori liniar independenți sunt suficienți:

cob de coordonate, і necoplanare vectori, luate din ordinul cântului, a stabilit sistem de coordonate afín al spațiului trivial :

Desigur, grila de coordonate „împletitură” nu este foarte la îndemână, dar sistemul de coordonate ne permite categoricînseamnă coordonatele oricărui vector și coordonatele oricărui punct din spațiu. Similar cu planul, în sistemul de coordonate afine spațiul nu prelucrează anumite formule despre care le-am ghicit deja.

Cea mai importantă și directă definiție a sistemului de coordonate afine este sistem de coordonate rectiliniu față de spațiu:

Punctul spațiului, așa cum se numește cob de coordonate, і ortonormalitati pune bazele Sistemul de coordonate rectiliniu cartezian . Cunoașteți imaginea:

Înainte de a trece la sarcinile practice, vom sistematiza din nou informațiile:

Pentru trei vectori din spațiu, aceleași solide sunt echivalente:
1) vectorii sunt liniar independenți;
2) vectorii definesc baza;
3) vectorii nu sunt coplanari;
4) vectorii nu pot fi exprimați liniar unul prin altul;
5) primar, plierea coordonatele acestor vectori, de la zero.

Leziunile de decubit, cred, s-au limpezit.

Localizarea/independența liniară a vectorilor în spațiu se verifică în mod tradițional cu ajutorul unei surse suplimentare (punctul 5). Cunoștințele practice care s-au pierdut sunt în mod clar de natură algebrică. Este timpul să atârnați o cheie geometrică de flori și să mânuiți algebra liniară cu o bâtă de baseball:

Trei spații vectoriale metode coplanare și numai cele, dacă originea, adunării coordonatelor acestor vectori, este egală cu zero: .

Aș dori să subliniez o mică nuanță tehnică: coordonatele vectorilor pot fi înregistrate nu numai în coloană, ci și în rând (valoarea celui primar nu se va schimba - puterea minunată a celor primari). Ale este mult mai frumoasă decât restul, ceea ce o face mai potrivită pentru îndeplinirea multor sarcini practice.

Acelor cititori care au uitat metodele de sortare a originalelor și s-ar putea să fi devenit prost orientați în ele, le recomand una dintre cele mai vechi lecții ale mele: Cum calculezi valoarea?

fundul 6

Verificați dacă următorii vectori creează baza spațiului trivial:

Decizie: De fapt, toate deciziile se reduc la plata principalului

a) Corolarul adunărilor din coordonatele vectorilor este calculabil (corolarul criteriilor din primul rând):

, De asemenea, vectorii sunt independenți liniar (nu coplanari) și creează baza unui spațiu trivial.

Vіdpovid: vectori de date și bază

b) Acesta este un punct de decizie independentă. Mai presus de toate, există o soluție și o concluzie la lecție.

Capcane și eforturi creative:

fundul 7

Pentru ce valoare a parametrului vor fi vectorii coplanari?

Decizie: Vectorii sunt coplanari și numai atunci, dacă originea, adăugarea coordonatelor acestor vectori este egală cu zero:

De fapt, este necesar să fii loial liderului. Ajungem la zerouri ca trucuri pe jerboas - cel mai evident este să-l deschidem pe alt rând și imediat vor fi minusuri:

Efectuăm o simplificare suplimentară și o reducem de la dreapta la cea mai simplă ecuație liniară:

Vіdpovid: la

Aici este ușor să efectuați o inversare, pentru care trebuie să înlocuiți valorile din sursa de ieșire și să reconvertiți astfel încât , după ce l-am deschis din nou.

În cele din urmă, ne vom uita la o altă problemă tipică, care este de natură mai algebrică și ar trebui inclusă înaintea cursului de algebră liniară. Partea de sus a mesei este lată, ceea ce merită următorul top:

Aduceți că 3 vectori creează baza spațiului trivial
și cunoașteți coordonatele celui de-al 4-lea vector în această bază

fundul 8

Vectori dați. Arătați că vectorii formează baza unui spațiu trivial și găsiți coordonatele vectorului în această bază.

Decizie: Să privim mai întâi mintea În spatele minții, există patru vectori și, după cum știți, există deja coordonate în aceeași bază. Aceasta este baza - nu ne deranja. Și pentru a spune astfel: trei vectori în ansamblu pot crea o nouă bază. Prima etapă este complet evitată din soluțiile din Anexa 6, este necesar să se verifice dacă vectorii sunt cu adevărat independenți liniar:

Covariata adunării coordonatelor vectorilor este calculabilă:

, De asemenea, vectorii sunt independenți liniar și creează baza unui spațiu trivial.

! Important : coordonate vectoriale obov'yazkovo inscriptibil în stație primul, și nu în rânduri. În caz contrar, va exista confuzie în continuarea algoritmului de dezlegare.

Viraz mintea numit combinație liniară de vectori A 1 , A 2 ,...,A n cu coeficienți λ 1, λ 2 ,...,λ n.

Valorile poziției liniare a sistemului vectorial

Sistem vectorial A 1 , A 2 ,...,A n numit liniar asezat pe spate, Ce este un set de numere diferit de zero? λ 1, λ 2 ,...,λ n, pentru orice combinație liniară de vectori λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n mai vechi decât vectorul zero, Apoi sistemul de ranguri: Există o decizie diferită de zero.
Formați numere λ 1, λ 2 ,...,λ n є diferit de zero, dacă doriți unul dintre numere λ 1, λ 2 ,...,λ n a schimba de la zero.

Valorile independenței liniare ale unui sistem vectorial

Sistem vectorial A 1 , A 2 ,...,A n numit liniar independent, ca o combinație liniară a acestor vectori λ 1 *A 1 +λ 2 *A 2 +...+λ n *A n mai mult decât un vector zero decât un set zero de numere λ 1, λ 2 ,...,λ n , Apoi sistemul de ranguri: A 1 x 1 +A 2 x 2 +...+A n x n =Θ Există o singură soluție.

Stoc 29.1

Verificați dacă acesta este un sistem liniar de vectori

Decizie:

1. Creăm un sistem de niveluri:

2. Verificat prin metoda Gaussiană. Transformarea sistemului Jordano este prezentată în Tabelul 29.1. Când partea dreaptă a sistemului este extinsă, fragmentele nu sunt înregistrate, ajung la zero și nu se modifică din cauza transformărilor Jordan.

3. Cele trei rânduri rămase ale tabelului înregistrează sistemul permis, egal cu rezultatul sistem:

4. Soluția ascunsă a sistemului este eliminată:

5. După ce a cerut autorităților valoarea schimbului liber x 3 =1, Deciziile non-zero sunt strict excluse X = (-3,2,1).

Dovezi: Astfel, cu o mulțime de numere nenule (-3,2,1), combinația liniară de vectori este egală cu vectorul zero -3A1+2A2+1A3=Θ. Otje, sistemul de vectori este dependent liniar.

Puterea sistemelor vectoriale

Putere (1)
Dacă un sistem de vectori este subordonat liniar, atunci dacă unul dintre vectori este descompus după ceilalți, atunci dacă unul dintre vectorii sistemului este descompus după ceilalți, sistemul de vectori este subordonat liniar.

Putere (2)
Deoarece fiecare subsistem de vectori este dependent liniar, atunci întregul sistem este dependent liniar.

Putere (3)
Dacă sistemul de vectori este liniar independent, atunci subsistemul este liniar independent.

Autoritate (4)
Indiferent dacă există un sistem de vectori care conține un vector zero, acesta este liniar învechit.

Autoritate (5)
Un sistem de vectori m-dimensionali este întotdeauna liniar, dacă numărul de vectori n este mai mare decât dimensiunea lor (n>m)

Baza sistemului vectorial

Baza sistemului vectorial A 1 , A 2 ,..., A n un astfel de subsistem se numește B 1 , B 2 ,..., B r(unul dintre vectorii B 1, B 2,..., B r este unul dintre vectorii A 1, A 2,..., A n), care satisface mințile zilei:
1. B 1 ,B 2 ,...,B r sistem liniar-independent de vectori;
2. indiferent de caz vector A j sistemele A 1 , A 2 ,..., A n sunt exprimate liniar prin vectorii B 1 , B 2 ,..., B r

r- Numărul de vectori incluși în bază.

Teorema 29.1 Despre baza unitară a unui sistem de vectori.

Dacă un sistem de vectori m-dimensionali conține m vectori unici diferiți E 1 E 2 ,..., E m , toți creează baza sistemului.

Algoritm pentru găsirea bazei unui sistem vectorial

Pentru a cunoaște baza sistemului vectorial A 1 , A 2 ,..., A n este necesar:

• Îndoiți un singur sistem de vectori într-un singur sistem de nivele A 1 x 1 +A 2 x 2 +...+A n x n =Θ
• Introduceți sistemul Qiu

O combinație liniară de vectori se numește vector
, de 1, ... , m - coeficienți suficienți.

Sistem vectorial
se numește liniar învechit deoarece combinația liniară principală este egală În acest caz, am dori un coeficient diferit de zero.

Sistem vectorial
se numește liniar independent, deoarece în orice combinație liniară care este veche toți coeficienții sunt zero.

Baza sistemului vectorial
Acesta se numește un subsistem nevid liniar independent, care poate fi definit ca un vector al sistemului.

Exemplul 2. Găsiți baza sistemului vectorial = (1, 2, 2, 4),= (2, 3, 5, 1),= (3, 4, 8, -2),= (2, 5, 0, 3) și exprimă alți vectori prin bază.

Rozv'yazannya. Să creăm o matrice în care coordonatele acestor vectori pot fi extinse cu coloane. Să o îndreptăm către o vedere pas cu pas.

~
~
~
.

Baza acestui sistem este determinată de vectori ,,, Care este reprezentată de elementele conductoare ale rândurilor, prezentate în cercuri. Pentru transformarea vectorială Probabil să fie egal x 1 +x 2 + x 4 =. Se reduce la un sistem de ranguri liniare, a cărui matrice reiese din permutarea de ieșire a coloanei, ceea ce demonstrează acolo are loc o întâlnire a membrilor liberi. Prin urmare, pentru a completa sistemul, matricea a fost extrasă din vedere treptat, făcându-se în ea permutările necesare.

Cunoscut în mod constant:

x1+4=3, x1=-1;

= -+2.

Nota 1. Dacă este necesar să se exprime pe baza unui număr de vectori, atunci pentru fiecare dintre ei va exista un sistem similar de niveluri liniare. Acest sistem va fi demontat doar de majoritatea membrilor săi. Prin urmare, pentru a le maximiza, puteți plia o matrice, care va conține un număr de membri diferiți. Al cărui sistem de piele este diferit de alții.

Respect 2. Pentru transformarea oricărui vector este suficient să vikorizăm vectorii de bază ai sistemului care stau în fața acestuia. În acest caz, nu este nevoie să remodelați matricea, este suficient să plasați o limită verticală în locația necesară.

2. Găsiți baza sistemului vectorial și exprimați alți vectori prin baza:

A) = (1, 3, 2, 0),= (3, 4, 2, 1),= (1, -2, -2, 1),= (3, 5, 1, 2);

b) = (2, 1, 2, 3),= (1, 2, 2, 3),= (3, -1, 2, 2),= (4, -2, 2, 2);

V) = (1, 2, 3),= (2, 4, 3),= (3, 6, 6),= (4, -2, 1);= (2, -6, -2).

1. 3. Sistem fundamental de soluții

Un sistem de ecuații liniare se numește omogen deoarece termenii săi liberi sunt egali cu zero.

Sistemul fundamental de decuplare a unui sistem cu un singur rând de niveluri liniare se numește baza impersonalității decuplărilor.

Permiteți-ne să vă oferim un sistem eterogen de ranguri liniare. Un singur sistem asociat cu o valoare este un sistem care este eliminat prin înlocuirea tuturor membrilor zero cu zerouri.

Deoarece sistemul eterogen este coerent și lipsit de importanță, atunci soluția sa mai satisfăcătoare arată ca f n +  1 f o1 + ... +  k f o k , def n – soluția privată a sistemului eterogen i f o1 , ... , f o k este fundamentală soluție de sistem a unui singur sistem asociat

PRI M E R 3. Aflați despre soluția unui sistem eterogen din Exemplul 1 și sistemul fundamental al unei soluții la un sistem omogen asociat.

Decizie. Notăm soluția, luată în Anexa 1, în formă vectorială și extindem vectorul care este cel mai mare, însumând parametrii suplimentari care se află în cel nou și valorile numerice fixe:

= (x 1 , x 2 , x 3 , x 4) = (–2a + 7b – 2, a, –2b + 1, b) = (–2a, a, 0, 0) + (7b, 0, – 2b, b) + + (-2, 0, 1, 0) = a (-2, 1, 0, 0) + b (7, 0, -2, 1) + (- 2, 0, 1, 0) ).

Eliminați f n = (-2, 0, 1, 0), f o1 = (-2, 1, 0, 0), f o2 = (7, 0, -2, 1).

Respect. În mod similar, este nevoie de a găsi un sistem fundamental pentru o soluție la un sistem omogen.

3.1 Cunoașteți sistemul fundamental și soluția unui sistem omogen:

A)

b)

c) 2x1 – x2+3x3=0.

EXERCIȚIUL 3.2. Aflați soluția privată a unui sistem eterogen și sistemul fundamental al unei soluții a unui sistem omogen asociat:

A)

b)

Găsiți baza sistemului de vectori și vectori care nu sunt incluși în bază, sortați după bază:

A 1 = {5, 2, -3, 1}, A 2 = {4, 1, -2, 3}, A 3 = {1, 1, -1, -2}, A 4 = {3, 4, -1, 2}, A 5 = {13, 8, -7, 4}.

Decizie. Să aruncăm o privire la un singur sistem de ranguri liniare

A 1 X 1 + A 2 X 2 + A 3 X 3 + A 4 X 4 + A 5 X 5 = 0

sau aspectul încins .

Verificăm acest sistem prin metoda Gaussiană, fără a alterna rânduri și coloane și, în plus, selectând elementul cap nu în colțul din stânga sus, ci pe întregul rând. Sălbăticia constă în faptul că vezi partea diagonală a sistemului vectorial transformat.

~ ~

~ ~ ~ .

Sistemul de vectori este permis, este egal cu ieșirea, se pare

A 1 1 X 1 + A 2 1 X 2 + A 3 1 X 3 + A 4 1 X 4 + A 5 1 X 5 = 0 ,

de A 1 1 = , A 2 1 = , A 3 1 = , A 4 1 = , A 5 1 = . (1)

Vectori A 1 1 , A 3 1 , A 4 1 stabiliți sistemul diagonal. Ozhe, vectori A 1 , A 3 , A 4 stabilesc baza sistemului vectorial A 1 , A 2 , A 3 , A 4 , A 5 .

Vectori depliabil acum A 2 і A 5 în spatele bazei A 1 , A 3 , A 4 . Pentru care sunt așezați următorii vectori A 2 1 і A 5 1 în spatele sistemului diagonal A 1 1 , A 3 1 , A 4 1 ținând cont de faptul că coeficienții descompunerii vectoriale de-a lungul sistemului diagonal al coordonatelor sale x i.

Z (1) maєmo:

A 2 1 = A 3 1 · (-1) + A 4 1 0 + A 1 1 ·1 => A 2 1 = A 1 1 – A 3 1 .

A 5 1 = A 3 1 0 + A 4 1 1 + A 1 1 ·2 => A 5 1 = 2A 1 1 + A 4 1 .

Vectori A 2 і A 5 pliază în spatele bazei A 1 , A 3 , A 4 cu aceiași coeficienți, care vectori A 2 1 і A 5 1 în spatele sistemului diagonal A 1 1 , A 3 1 , A 4 1 (acei coeficienți x i). Otje,

A 2 = A 1 – A 3 , A 5 = 2A 1 + A 4 .

Zavdannya. 1.Găsiți baza sistemului de vectori și vectori care nu sunt incluși în bază, sortați după bază:

1. A 1 = { 1, 2, 1 }, A 2 = { 2, 1, 3 }, A 3 = { 1, 5, 0 }, A 4 = { 2, -2, 4 }.

2. A 1 = { 1, 1, 2 }, A 2 = { 0, 1, 2 }, A 3 = { 2, 1, -4 }, A 4 = { 1, 1, 0 }.

3. A 1 = { 1, -2, 3 }, A 2 = { 0, 1, -1 }, A 3 = { 1, 3, 0 }, A 4 = { 0, -7, 3 }, A 5 = { 1, 1, 1 }.

4. A 1 = { 1, 2, -2 }, A 2 = { 0, -1, 4 }, A 3 = { 2, -3, 3 }.

2. Găsiți toate bazele sistemului vectorial:

1. A 1 = { 1, 1, 2 }, A 2 = { 3, 1, 2 }, A 3 = { 1, 2, 1 }, A 4 = { 2, 1, 2 }.

2. A 1 = { 1, 1, 1 }, A 2 = { -3, -5, 5 }, A 3 = { 3, 4, -1 }, A 4 = { 1, -1, 4 }.