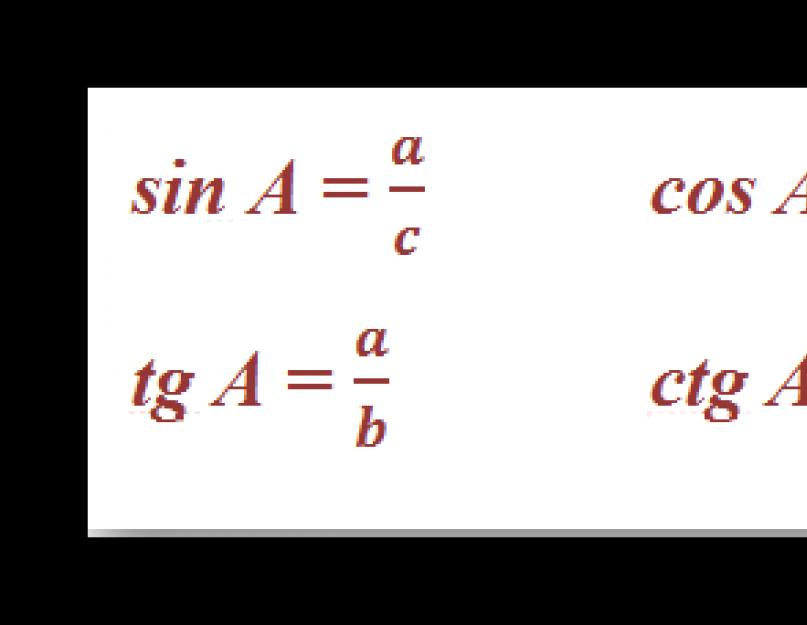Тригонометрія, як наука, зародилася на Стародавньому Сході. Перші тригонометричні співвідношення були виведені астрономами для створення точного календаря та орієнтування за зірками. Дані обчислення належали до сферичної тригонометрії, тоді як у шкільному курсі вивчають співвідношення сторін та кута плоского трикутника.
Тригонометрія – це розділ математики, що займається властивостями тригонометричних функцій та залежністю між сторонами та кутами трикутників.
У період розквіту культури та науки I тисячоліття нашої ери знання поширилися з Стародавнього Сходу до Греції. Але основні відкриття тригонометрії – заслуга чоловіків арабського халіфату. Зокрема, туркменський учений аль-Маразві ввів такі функції, як тангенс та котангенс, склав перші таблиці значень для синусів, тангенсів та котангенсів. Поняття синуса та косинуса введено індійськими вченими. Тригонометрії присвячено чимало уваги у працях таких великих діячів давнини, як Евкліда, Архімеда та Ератосфена.
Основні величини тригонометрії
Основні тригонометричні функції числового аргументу – це синус, косинус, тангенс та котангенс. Кожна з них має свій графік: синусоїда, косінусоїда, тангенсоїда та котангенсоїда.
У основі формул до розрахунку значень зазначених величин лежить теорема Піфагора. Школярам вона більше відома у формулюванні: «Піфагорові штани, на всі боки рівні», оскільки доказ наводиться на прикладі рівнобедреного прямокутного трикутника.
Синус, косинус та інші залежності встановлюють зв'язок між гострими кутами та сторонами будь-якого прямокутного трикутника. Наведемо формули для розрахунку цих величин для кута A і простежимо взаємозв'язки тригонометричних функцій:

Як видно, tg та ctg є зворотними функціями. Якщо уявити катет a як добуток sin A та гіпотенузи с, а катет b у вигляді cos A * c, то отримаємо такі формули для тангенсу та котангенсу:

Тригонометричне коло
Графічно співвідношення згаданих величин можна так:

Окружність, у разі, є всі можливі значення кута α — від 0° до 360°. Як видно з малюнка, кожна функція набуває негативного або позитивного значення в залежності від величини кута. Наприклад, sin α буде зі знаком «+», якщо α належить І і ІІ чверті кола, тобто знаходиться у проміжку від 0° до 180°. При від 180° до 360° (III і IV чверті) sin α може бути тільки негативним значенням.
Спробуємо побудувати тригонометричні таблиці для конкретних кутів та дізнатися значення величин.

Значення α рівні 30°, 45°, 60°, 90°, 180° тощо – називають окремими випадками. Значення тригонометричних функцій їм прораховані і представлені у вигляді спеціальних таблиць.

Ці кути обрані зовсім не випадково. Позначення π у таблицях стоїть для радіан. Радий - це кут, при якому довжина дуги кола відповідає її радіусу. Дана величина була введена для того, щоб встановити універсальну залежність, при розрахунках у радіанах не має значення дійсна довжина радіуса см.

Кути в таблицях для тригонометричних функцій відповідають значенням радіан:

Отже, не важко здогадатися, що 2π - це повне коло або 360 °.
Властивості тригонометричних функцій: синус та косинус
Для того, щоб розглянути та порівняти основні властивості синуса та косинуса, тангенсу та котангенсу, необхідно накреслити їх функції. Зробити це можна у вигляді кривої, розташованої у двовимірній системі координат.
Розглянь порівняльну таблицю властивостей для синусоїди та косінусоїди:

| Синусоїда | Косинусоїда |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, де k ϵ Z | cos x = 0 при x = π/2 + πk, де k ϵ Z |
| sin x = 1, за x = π/2 + 2πk, де k ϵ Z | cos x = 1 при x = 2πk, де k ϵ Z |
| sin x = - 1 при x = 3π/2 + 2πk, де k ϵ Z | cos x = - 1 при x = π + 2πk, де k ϵ Z |
| sin (-x) = - sin x, тобто функція непарна | cos (-x) = cos x, тобто функція парна |
| функція періодична, найменший період - 2π | |
| sin x › 0, при x належить I і II чвертям або від 0° до 180° (2πk, π + 2πk) | cos x › 0, при x належить I і IV чвертям або від 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x належить III і IV чвертям або від 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x належить II і III чвертям або від 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| зростає на проміжку [- π/2 + 2πk, π/2 + 2πk] | зростає на проміжку [-π + 2πk, 2πk] |
| зменшується на проміжках [ π/2 + 2πk, 3π/2 + 2πk] | зменшується на проміжках |
| похідна (sin x)’ = cos x | похідна (cos x)' = - sin x |
Визначити чи є функція парною чи ні дуже просто. Достатньо уявити тригонометричний круг зі знаками тригонометричних величин і подумки «скласти» графік щодо осі OX. Якщо знаки збігаються, функція парна, інакше непарна.

Введення радіан та перерахування основних властивостей синусоїди та косінусоїди дозволяють навести наступну закономірність:

Переконатись у вірності формули дуже просто. Наприклад, для x = π/2 синус дорівнює 1, як і косинус x = 0. Перевірку можна здійснити звернули до таблиць або простеживши криві функцій для заданих значень.
Властивості тангенсоїди та котангенсоїди
Графіки функцій тангенсу та котангенсу значно відрізняються від синусоїди та косинусоїди. Величини tg та ctg є зворотними один одному.


- Y = tg x.
- Тангенсоіда прагне значень y при x = π/2 + πk, але ніколи не досягає їх.
- Найменший позитивний період тангенсоіди дорівнює π.
- Tg (-x) = - tg x, тобто функція непарна.
- Tg x = 0 при x = πk.
- Функція є зростаючою.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Похідна (tg x)' = 1/cos 2 x .
Розглянемо графічне зображення котангенсоіди нижче за текстом.

Основні властивості котангенсоіди:
- Y = ctg x.
- На відміну від функцій синуса і косинуса, в тангенсоіді Y може набувати значення безлічі всіх дійсних чисел.
- Котангенсоіда прагне значень y при x = πk, але ніколи не досягає їх.
- Найменший позитивний період котангенсоіди дорівнює π.
- Ctg (-x) = - ctg x, тобто функція непарна.
- Ctg x = 0, при x = π/2 + πk.
- Функція є спадною.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Похідна (ctg x)’ = — 1/sin 2 x Виправити
Спочатку синус і косинус виникли через необхідність розраховувати величини прямокутних трикутниках. Було помічено, що й значення градусної міри кутів у прямокутному трикутнику не змінювати, то співвідношення сторін, хоч би ці сторони змінювалися у довжині, залишається завжди однаковим.
Саме так і було введено поняття синуса та косинуса. Синус гострого кута у прямокутному трикутнику – це відношення протилежного катета до гіпотенузи, а косинус – прилеглого до гіпотенузи.
Теореми косінусів та синусів
Але косинуси та синуси можуть застосовуватися не тільки у прямокутних трикутниках. Щоб знайти значення тупого чи гострого кута, сторони будь-якого трикутника, достатньо застосувати теорему косінусів та синусів.
Теорема косінусів досить проста: «Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін за вирахуванням подвоєного твору цих сторін на косинус кута між ними».
Існує два трактування теореми синусів: мала та розширена. Відповідно до малої: «У трикутнику кути пропорційні протилежним сторонам». Цю теорему часто розширюють за рахунок властивості описаного у трикутника кола: «У трикутнику кути пропорційні протилежним сторонам, а їх відношення дорівнює діаметру описаного кола».
Похідні
Похідна – математичний інструмент, що показує, як швидко змінюється функція щодо зміни її аргументу. Похідні використовуються , геометрії, і ряд технічних дисциплін.
При вирішенні завдань потрібно знати табличні значення похідних тригонометричних функцій: синуса та косинуса. Похідною синуса є косинус, а косинуса – синус, але зі знаком «мінус».
Застосування в математиці
Особливо часто синуси та косинуси використовуються при вирішенні прямокутних трикутників та завдань, пов'язаних з ними.
Зручність синусів і косінусів знайшло своє відображення і в техніці. Кути та сторони було просто оцінювати за теоремами косинусів та синусів, розбиваючи складні фігури та об'єкти на «прості» трикутники. Інженери і , що часто мають справу з розрахунками співвідношення сторін і градусних заходів, витрачали чимало часу та зусиль для обчислення косінусів та синусів не табличних кутів.
Тоді «на допомогу» прийшли таблиці Брадіса, що містять тисячі значень синусів, косінусів, тангенсів та котангенсів різних кутів. За радянських часів деякі викладачі змушували своїх підопічних сторінки таблиць Брадіса напам'ять.
Радіан - кутова величина дуги, по довжині рівної радіусу або 57,295779513 градусів.
Градус (в геометрії) - 1/360 частина кола або 1/90 частина прямого кута.
π = 3.141592653589793238462… (приблизне значення числа Пі).
Косинус – це відома тригонометрична функція, яка до того ж є ще й однією з основних функцій тригонометрії. Косинус кута в трикутнику прямокутного типу - це відношення прилеглого катета трикутника до гіпотенузи трикутника. Найчастіше визначення косинуса пов'язують із трикутником саме прямокутного типу. Але буває і так, що той кут, для якого необхідно обчислити в трикутнику прямокутного типу косинус, у цьому трикутнику прямокутного типу не розташований. Що тоді робити? Як знайти косинус кута трикутника?
Якщо потрібно обчислити косинус кута саме в трикутнику прямокутного типу, то все дуже просто. Потрібно лише згадати визначення косинуса, у якому криється вирішення цього завдання. Просто потрібно знайти те саме ставлення між прилеглим катетом, а також гіпотенузою трикутника. Справді, тут неважко висловити косинус кута. Формула виглядає так: - cosα = a/c, тут "а" - це довжина катета, а сторона "с", відповідно, довжина гіпотенузи. Наприклад, косинус гострого кута прямокутного трикутника можна знайти за цією формулою.
Якщо Вас цікавить, до чого дорівнює косинус кута в довільному трикутнику, то на допомогу приходить теорема косінусів, якою і варто скористатися в подібних випадках. Теорема косінусів говорить про те, що квадрат сторони трикутника апріорі дорівнює сумі квадратів інших сторін того ж трикутника, але вже без подвоєного добутку цих сторін на косинус того кута, який розташований між ними.
- Якщо у трикутнику необхідно знайти косинус гострого кута, то потрібно скористатися такою формулою: cosα = (a 2 + b 2 – c 2)/(2ab).
- Якщо ж у трикутнику необхідно знайти косинус тупого кута, потрібно скористатися такою формулою: cosα = (з 2 – a 2 – b 2)/(2ab). Позначення у формулі – а та b – це довжини сторін, які є прилеглими до шуканого кута, с – це довжина сторони, яка є протилежною шуканому куту.
Також косинус кута можна обчислювати за допомогою теореми синусів. Вона свідчить, що це сторони трикутника пропорційні синусам кутів, які протилежні. За допомогою теореми синусів можна обчислювати решту елементів трикутника, маючи відомості лише про дві сторони і вугілля, що є протилежним одній стороні, або ж по двох кутах і одній стороні. Розглянь на прикладі. Умови задачі: а = 1; b = 2; с=3. Кут, який протилежний стороні "А", позначаємо - α, тоді, згідно з формулами, маємо: соsα=(b²+c²-а²)/(2*b*c)=(2²+3²-1²)/(2*2 *3)=(4+9-1)/12=12/12=1. Відповідь: 1.
Якщо ж косинус кута потрібно обчислити над трикутнику, а якийсь інший довільної геометричній фігурі, то тут усе стає трохи складніше. Величину кута спочатку потрібно визначити в радіанах або градусах, а вже потім обчислювати косинус за цією величиною. Косинус за числовим значенням визначається за допомогою таблиць Брадіса, інженерних калькуляторів або спеціальних математичних програм.
Спеціальні математичні програми можуть мати такі функції, як автоматичний підрахунок косінусів кутів у тій чи іншій фігурі. Принадність таких додатків полягає в тому, що вони дають правильну відповідь, а користувач не витрачає свого часу на вирішення часом досить складних завдань. З іншого боку, при постійному використанні виключно додатків для розв'язання задач, губляться всі навички по роботі з розв'язанням математичних задач на знаходження косінусів кутів у трикутниках та інших довільних фігурах.
Тригонометрія є розділом математики, що вивчає тригонометричні функції, а також їх використання на практиці. До таких функцій відносяться синус, косинус, тангенс та котангенс.
Синус – це тригонометрична функція, Відношення величини протилежного катета до величини гіпотенузи
Синус у тригонометрії.
Як уже сказано вище, синус має безпосереднє відношення до тригонометрії та тригонометричних функцій. Його функція визначається тим, щоб
- допомагати розрахувати кут, за умови популярності величин сторін трикутника;
- допомагати вирахувати величини сторони трикутника, за умови популярності кута.
Необхідно пам'ятати, що величина синуса завжди однакова для будь-яких розмірів трикутника, оскільки синус – це не вимір, а співвідношення.
Отже, щоб не вираховувати цю постійну величину при кожному вирішенні тієї чи іншої завдання, були створені спеціальні тригонометричні таблиці. Вони величини синусів, косінусів, тангенсів і котангенсів вже прораховані і закріплені. Зазвичай ці таблиці наводяться на форзаці підручників з алгебри та геометрії. Також їх можна знайти в Інтернеті.
Синус у геометрії.
Геометрія вимагає наочності, тому, щоб зрозуміти на практиці, що таке синус кутапотрібно намалювати трикутник з прямим кутом.
Припустимо, що сторони, що утворюють прямий кут, названі а, в,протилежний їм кут – х.
Зазвичай у завданнях вказано довжину сторін. Припустимо, а = 3, = 4. У такому разі співвідношення сторін виглядатиме як ¾. При цьому якщо подовжити сторони трикутника, що прилягають до гострого кута х, то збільшаться і сторони аі ві гіпотенуза – третя сторона прямокутного трикутника, що лежить не під прямим кутом до основи. Тепер сторони трикутника можна назвати інакше, скажімо: m, n, k.
У цьому видозміні спрацював закон тригонометрії: довжини сторін трикутника змінилися, які ставлення – немає.
Той факт, що при зміні довжини сторін трикутника у скільки завгодно разів і при збереженні величини кута х, співвідношення між його сторонами все одно залишиться незмінним, помітили ще давні вчені. У нашому випадку довжина сторін могла змінитися так: а/в = ¾, при подовженні сторони адо 6 см, а в- До 8 см отримуємо: m/n = 6/8 = 3/4.
Співвідношення сторін у прямокутному трикутнику у зв'язку з цим отримали назви:
- синус кута х - це відношення протилежного катета до гіпотенузи: sinx = а / с;
- косинус кута х – це відношення прилеглого катета до гіпотенузи: сosx = в/с;
- тангенс кута х – це відношення протилежного катета до прилеглого: tgx = а/в;
- котангенс кута х – це відношення прилеглого катета до протилежного: ctgx = в/а.
Тригонометрія - розділ математичної науки, в якому вивчаються тригонометричні функції та їх використання у геометрії. Розвиток тригонометрії почався ще за часів античної Греції. За часів середньовіччя важливий внесок у розвиток цієї науки зробили вчені Близького Сходу та Індії.
Ця стаття присвячена базовим поняттям та визначенням тригонометрії. У ній розглянуто визначення основних тригонометричних функцій: синуса, косинуса, тангенсу та котангенсу. Роз'яснено та проілюстровано їх зміст у контексті геометрії.
Спочатку визначення тригонометричних функцій, аргументом яких є кут, виражалися через співвідношення сторін прямокутного трикутника.
Визначення тригонометричних функцій
Синус кута (sin α) - відношення катета, що протилежить цьому куту, до гіпотенузи.
Косинус кута (cos α) – відношення прилеглого катета до гіпотенузи.
Тангенс кута (t g α) - відношення протилежного катета до прилеглого.
Котангенс кута (c t g α) - відношення прилеглого катета до протилежного.
Дані визначення дано для гострого кута прямокутного трикутника!
Наведемо ілюстрацію.
У трикутнику ABC з прямим кутом С синус кута дорівнює відношенню катета BC до гіпотенузи AB.
Визначення синуса, косинуса, тангенсу та котангенсу дозволяють обчислювати значення цих функцій за відомими довжинами сторін трикутника.
Важливо пам'ятати!
Область значень синуса і косинуса: від -1 до 1. Іншими словами синус і косинус набувають значення від -1 до 1. Область значень тангенсу та котангенсу - вся числова пряма, тобто ці функції можуть набувати будь-яких значень.
Визначення, дані вище, відносяться до гострих кутів. У тригонометрії вводиться поняття кута повороту, величина якого, на відміну від гострого кута, не обмежена рамками від 0 до 90 градусів.
У цьому контексті можна дати визначення синуса, косинуса, тангенсу та котангенсу кута довільної величини. Уявімо одиничне коло з центром на початку декартової системи координат.

Початкова точка A з координатами (1 , 0) повертається навколо центру одиничного кола на деякий кут і переходить в точку A 1 . Визначення дається через координати точки A 1 (x, y).
Синус (sin) кута повороту
Синус кута повороту - це ордината точки A 1 (x, y). sin α = y
Косинус (cos) кута повороту
Косинус кута повороту α - це абсцис точки A 1 (x, y). cos α = х
Тангенс (tg) кута повороту
Тангенс кута повороту - це відношення ординати точки A 1 (x, y) до її абсцисі. t g α = y x
Котангенс (ctg) кута повороту
Котангенс кута повороту - це відношення абсциси точки A 1 (x, y) до її ординаті. c t g α = x y
Синус та косинус визначені для будь-якого кута повороту. Це логічно, адже абсцису та ординату точки після повороту можна визначити за будь-якого вугілля. Інакше справа з тангенсом і котангенсом. Тангенс не визначено, коли точка після повороту перетворюється на точку з нульовою абсцисою (0 , 1) і (0 , - 1). У таких випадках вираз для тангенсу t g α = y x просто не має сенсу, оскільки в ньому є поділ на нуль. Аналогічно ситуація із котангенсом. Відмінністю у тому, що котангенс не визначено у випадках, як у нуль звертається ордината точки.
Важливо пам'ятати!
Синус та косинус визначені для будь-яких кутів α.
Тангенс визначений для всіх кутів, крім α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс визначений для всіх кутів, крім α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При вирішенні практичних прикладів не говорять "синус кута повороту". Слова "кут повороту" просто опускають, маючи на увазі, що з контексту і так зрозуміло, про що йдеться.
Числа
Як бути з визначенням синуса, косинуса, тангенсу та котангенсу числа, а не кута повороту?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом і котангенсом числа tназивається число, яке відповідно дорівнює синусу, косинусу, тангенсу та котангенсу в tрадіан.
Наприклад, синус числа 10 π дорівнює синусу кута повороту величиною 10 π рад.
Існує й інший підхід до визначення синуса, косинуса, тангенсу та котангенсу числа. Розглянемо його докладніше.
Будь-якому дійсному числу tставиться у відповідність точка на одиничному колі з центром на початку прямокутної декартової системи координат. Синус, косинус, тангенс та котангенс визначаються через координати цієї точки.
Початкова точка на колі - точка A з координатами (1, 0).
Позитивного числа t
Негативному числу tвідповідає точка, в яку перейде початкова точка, якщо рухатиметься по колу проти годинникової стрілки та пройде шлях t .
Тепер, коли зв'язок числа та точки на колі встановлено, переходимо до визначення синуса, косинуса, тангенсу та котангенсу.
Синус (sin) числа t
Синус числа t- ордината точки одиничного кола, що відповідає числу t. sin t = y
Косинус (cos) числа t
Косинус числа t- абсцису точки одиничного кола, що відповідає числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t- відношення ординати до абсцису точки одиничного кола, що відповідає числу t. t g t = y x = sin t cos t
Останні визначення знаходяться у відповідності та не суперечать визначенню, даному на початку цього пункту. Крапка на колі, що відповідає числу tзбігається з точкою, в яку переходить початкова точка після повороту на кут tрадіан.
Тригонометричні функції кутового та числового аргументу
Кожному значенню кута відповідає певне значення синуса і косинуса цього кута. Також, як усім кутам α, відмінним від α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) відповідає певне значення тангенсу. Котангенс, як сказано вище, визначений для всіх α, крім α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можна сказати, що sin α, cos α, t g α, c t g α - це функції кута альфа, або функції кутового аргументу.
Аналогічно можна говорити про синус, косинус, тангенс і котангенс, як про функції числового аргументу. Кожному дійсному числу tвідповідає певне значення синуса чи косинуса числа t. Усім числам, відмінним від π 2 + π · k, k ∈ Z відповідає значення тангенсу. Котангенс, аналогічно, визначено всім чисел, крім π · k , k ∈ Z.
Основні функції тригонометрії
Синус, косинус, тангенс та котангенс - основні тригонометричні функції.
З контексту зазвичай зрозуміло, з яким аргументом тригонометричної функції (кутовий аргумент чи числовий аргумент) ми маємо справу.
Повернемося до даних на самому початку визначенням та кутку альфа, що лежить у межах від 0 до 90 градусів. Тригонометричні визначення синуса, косинуса, тангенсу та котангенсу повністю узгоджуються з геометричними визначеннями, даними за допомогою співвідношень сторін прямокутного трикутника. Покажемо це.

Візьмемо одиничне коло з центром у прямокутній декартовій системі координат. Повернемо початкову точку A(1,0) на кут величиною до 90 градусів і проведемо з отриманої точки A1(x, y) перпендикуляр до осі абсцис. В отриманому прямокутному трикутнику кут A 1 O H дорівнює куту повороту α довжина катета O H дорівнює абсцисі точки A 1 (x , y) . Довжина катета, що протилежить куту, дорівнює ординаті точки A 1 (x , y), а довжина гіпотенузи дорівнює одиниці, оскільки вона є радіусом одиничного кола.
Відповідно до визначення з геометрії, синус кута α дорівнює відношенню протилежного катета до гіпотенузи.
sin α = A 1 H O A 1 = y 1 = y
Значить, визначення синуса гострого кута в прямокутному трикутнику через співвідношення сторін еквівалентно визначенню синуса кута повороту α при альфа лежить в межах від 0 до 90 градусів.
Аналогічно відповідність визначень можна показати для косинуса, тангенсу та котангенсу.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter