Визначення перпендикулярних прямих

Перпендикулярні до прямих.

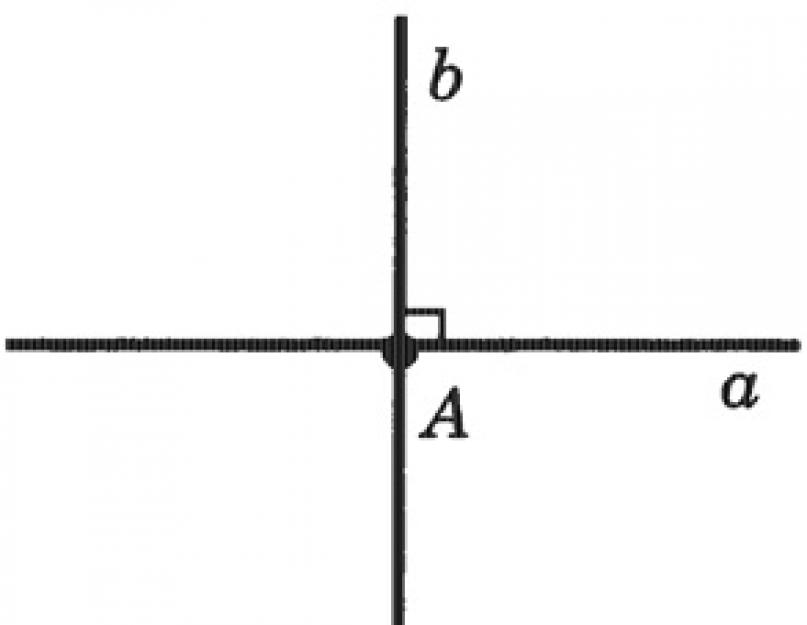
Нехай а та b - прямі, що перетинаються в точці А (рис. 1). Кожна з цих прямих точкою А ділиться на дві напівпрямі. Напівпрямі однієї прямої утворюють з напівпрямими інший прямий чотири кути. Нехай альфа - один із цих кутів. Тоді будь-який з трьох кутів буде або суміжним з кутом альфа, або вертикальним з кутом альфа.

Звідси випливає, що й один з кутів прямий, інші кути теж будуть прямі, У разі ми говоримо, що прямі перетинаються під прямим кутом.
Визначення.
Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом (рис. 2).

Перпендикулярність прямих позначається знаком ⊥ Запис а ⊥ b читається: Пряма а перпендикулярна до прямої b.
Теорема.

Через кожну точку прямої можна провести перпендикулярну їй пряму, і лише одну.

Доведення.
Нехай а - ця пряма і А - дана точка на ній. Позначимо через ах одну з напівпрямих прямою а з початковою точкою А (рис. 3). Відкладемо від напівпрямої а1 кут (a1b1), що дорівнює 90°.
Тоді пряма, що містить промінь b1, буде перпендикулярна до прямої а.

Припустимо, що існує інша пряма, яка проходить через точку А і перпендикулярна до прямої а. Позначимо через с1 напівпряму цієї прямої, що лежить в одній напівплощині з променем b2. Кути (a1b1) та (a1c1), рівні кожен 90°, відкладені в одну напівплощину від напівпрямої а1. Але від напівпрямої а1 у цю напівплощину можна відкласти лише один кут, що дорівнює 90°. Тому не може бути іншої прямої, яка проходить через точку А і перпендикулярна до прямої а. Теорему доведено.

Визначення.

Перпендикуляром до цієї прямої називається відрізок прямої, перпендикулярної даної, який має одним зі своїх кінців їх точку перетину. Цей кінець відрізка називається основою перпендикуляра.
На малюнку 4 перпендикуляр АВ проведено з точки А до прямої а. Точка В - основа перпендикуляра.

Для побудови перпендикуляра користуються креслярським косинцем (рис. 5).

Дві прямі, що перетинаються, називаються перпендикулярними (або взаємно перпендикулярними), якщо вони утворюють чотири прямі кути. Перпендикулярність прямих АС та ВD позначається так: АС ⊥ ВD (читається: «Пряма АС перпендикулярна до прямої ВD»).
Зазначимо, що дві прямі, перпендикулярні до третьої, не перетинаються (рис. 6, а). Справді, розглянемо прямі АА1 та ВВ1, перпендикулярні до прямої РQ (рис. 6, б). Подумки перегнемо малюнок по прямій РQ так, щоб верхня частина малюнка наклалася на нижню. Оскільки прямі кути 1 і 2 рівні, то промінь РА накладеться на промінь РА1. Аналогічно, промінь QВ накладеться на промінь QB1. Тому, якщо припустити, що прямі АА1 і ВВ1 перетинаються в точці М, то ця точка накладеться на деяку точку М1, що також лежить на цих прямих (рис. 6, в), і ми отримаємо, що через точки М і М1 проходять дві прямі: АА1 та ВВ1. Але це неможливо. Отже, наше припущення є невірним і, отже, прямі АА1 і ВВ1 не перетинаються.

Побудова прямих кутів біля

Для побудови прямих кутів біля застосовують спеціальні прилади, найпростішим з яких є екер. Екер являє собою два бруски, розташовані під прямим кутом і укріплені на триніжку (рис. 7). На кінцях брусків вбиті цвяхи отже прямі, які проходять них, взаємно перпендикулярні. Щоб побудувати на місцевості прямий кут із заданою стороною ОА, встановлюють триніжок з екером так, щоб схил знаходився точно над точкою О, а напрям одного бруска збігся з напрямком променя ОА. Поєднання цих напрямів можна здійснити за допомогою віхи, поставленої на промені. Потім провішують пряму лінію у напрямку іншого бруска (пряма ОВ малюнку 7). Виходить прямий кут АОВ.
У геодезії для побудови прямих кутів використовуються досконаліші прилади, наприклад, теодоліт.

По горизонталі:
3 . Відрізок прямий, що з'єднує точку кола з її центром. 6 . Твердження, яке вимагає докази. 9 . Конструкція, система думок. 10 . Вигляд чотирикутника. 15 . Відрізок прямий, що з'єднує дві точки кривій. 16 . Міра довжини. 17 18 . Точка перетину діаметрів кола. 19 . Тригонометрична функція. 20 . Частина кола. 21 . Урожай міра довжини.
По вертикалі:
1 . Символ будь-якого алфавіту. 2 . Перегляд паралелограма. 4 . Хорда, що проходить через центр кола. 5 . Геометричні елемент. 7 . Промінь, що ділить кут навпіл. 8 . Грецька абетка символ. 10 . Сума довжин сторін трикутника. 11 . Допоміжна пропозиція, яка використовується для доказу. 12 . Елемент прямокутного трикутника. 13 . Одна із чудових ліній трикутника. 14 . Тригонометрична функція.

Є таке завдання:

У Зачарованому Лісі було 10 зачарованих джерел - номер 1, 2, 3,... 10. Вода кожного джерела була невідмінна на колір, смак і запах від звичайної води, але була найсильнішою отрутою. Випив її був приречений - якщо тільки протягом години після цього не пив води джерела з більшим номером (наприклад, від отрути джерела 3 рятували джерела 4-10; отрута 10-го джерела не залишала шансів на псування). Перші 9 джерел були загальнодоступні, але джерело 10 було у печері Кащея Безсмертного, і доступом до нього мав лише Кащей.
І ось одного дня Іван-Дурак викликав Кащея на поєдинок. Умови були простими: кожен приносить із собою по склянці деякої рідини, суперники обмінюються склянками та випивають їх вміст. А далі – справляються, як можуть.
Кащій був задоволений. Ще б пак: він дасть Івану отруту номер 10, і Івана ніщо не зможе врятувати. А сама отрута, дана Іваном, зап'є водою 10-го джерела - і буде врятована.
Спробуйте розробити план дуелі для Івана. Завдання - залишитися жити самому і закінчити Кащея.

Відповідь 1. Погрожувати Кащея. Йому треба дати не отруту, а чисту воду. Він зап'є її своєю отрутою - і він приречений.
Відповідь 2. Не загрожувати самому. Будь-яка отрута, крім номера 1, може бути і отрутою. Перед тим, як прийти на дуель, потрібно випити отруту малого номера. І тоді отрута номер 10, отримана від Кащея на дуелі, не вб'є, а врятує.

Взагалі, ідея тривіальна. Не завжди можна зважити вчинок ізольовано. Одна і та ж дія може виявитися і отрутою, і протиотрутою. Багато залежить від фону. Не говоритиму, що все - але, безсумнівно, багато.
І коли ви чуєте, що хтось із ваших знайомих здійснив Таку-то і таку-то гідність, не поспішайте вішати ярлики. Чи ви впевнені, що це саме гидоти? Чи не може бути, що вони так виглядають? Чи ви впевнені, що фон цих дій вам відомий?

Побудова перпендикулярної прямої

Зараз ми з вами за допомогою циркуля спробуємо збудувати перпендикулярну пряму. Для цього ми маємо точку О і пряму а.

На першому малюнку зображено пряму на якій лежить точка О, а на другому дана точка не лежить на прямій а.

Тепер давайте окремо розглянемо ці обидва варіанти.

1-й варіант

Спочатку ми беремо циркуль, ставимо його в центр точки О і креслимо коло з довільним радіусом. Тепер бачимо, що це коло перетинає пряму а двох точках. Нехай це будуть точки А та В.

Далі, ми беремо і проводимо кола з точок А і В. Радіус цих кіл буде АВ, а ось точка С буде точкою перетину цих кіл. Якщо ви пам'ятаєте, то на початку ми з вами отримали точки А і В, коли креслили коло і брали довільний радіус.

У результаті бачимо, що шукана перпендикулярна пряма проходить через точки З і З.

Доведення

Для цього нам потрібно провести відрізки AC і CB. І ми бачимо, що трикутники, що утворилися, рівні: Δ ACO = Δ BCO, це випливає з третьої ознаки рівності трикутників, тобто у нас виходить, що AO = OB, AC = CB, а СО загальна за побудовою. Кути, що утворилися ∠ COA і ∠ COB рівні і обидва мають величину, рівну 90 °. З цього випливає, що пряма CO перпендикулярна до AB.

Звідси ми можемо зробити висновок, що кути, утворені при перетині двох прямих, є перпендикулярними в тому випадку, якщо хоча б один з них перпендикулярний, а це означає, що такий кут дорівнює 90 градусам і є прямим.

2-й варіант

А тепер давайте розглянемо варіант побудови перпендикулярної прямої, де ця точка не лежить на прямій а.

У цьому випадку ми за допомогою циркуля з точки Про проводимо коло з таким радіусом, щоб це коло перетинала пряму а. А точки А і В нехай будуть точками перетину цього кола з даною прямою а.

Далі, ми беремо такий же радіус, але проводимо кола, центром яких будуть точки A і B. Дивимося на малюнок і бачимо, що у нас з'явилася точка О1, яка також є точкою перетину кіл і лежить у напівплощині, але відмінною від тієї, в якою знаходиться точка О.

Наступне, що ми зробимо, то через точки O і O1 проведемо пряму. Це і буде та перпендикулярна пряма, яку ми шукали.

Доведення

Припустимо, що точкою перетину прямих OO1 і AB є точка С. Тоді трикутники AOB і BO1A дорівнюють за третьою ознакою рівності трикутників і AO = OB = AO1 = O1B, а АВ є загальною за побудовою. З цього випливає, що кути OAС та O1AC рівні. Трикутники OAC та O1AC, виходячи з першої ознаки рівності трикутників AO дорівнює AO1, а за побудовою, кути OAС та O1AC рівні за загальної AС. Отже, що кут OСA дорівнює куту O1CA, але оскільки вони суміжні, тобто прямі. Тому робимо висновок, що OC є перпендикуляром, який опущений з точки O на пряму a.

Ось так, тільки за допомогою циркулю та лінійки, можна легко побудувати перпендикулярні прямі. І не важливо, де знаходиться точка, через яку повинен проходити перпендикуляр, на відрізку або поза цим відрізком, головне в цих випадках правильно знайти і позначити початкові точки А і В.

Запитання:

1. Які прямі називаються перпендикулярними?
2. Який кут між перпендикулярними прямими?
3. Чим користуються для побудови перпендикулярних до прямих?

Предмети > Математика > Математика 7 клас

Перпендикулярні прямі фігурують мало не в кожній геометричній задачі. Іноді перпендикулярність прямих відома з умови, а інших випадках перпендикулярність прямих доводиться доводити. Для доказу перпендикулярності двох прямих досить показати, використовуючи будь-які геометричні методи, що кут між прямими дорівнює дев'яноста градусам.

А як відповісти на запитання, чи «перпендикулярні прямі», якщо відомі рівняння, що задають ці прямі на площині або в тривимірному просторі?

Для цього слід скористатися необхідною та достатньою умовою перпендикулярності двох прямих. Сформулюємо його як теореми.

Теорема.

aі bнеобхідно і достатньо, щоб напрямний вектор прямий aбув перпендикулярний напрямному вектору прямий b.

Доказ цієї умови перпендикулярності прямих ґрунтується на визначенні напрямного вектора прямої та на визначенні перпендикулярних прямих.

Додамо конкретики.

Нехай на площині введено прямокутну декартову систему координат Oxyі задані рівняння прямої на площині деякого виду, що визначають прямі aі b. Позначимо напрямні вектори прямих аі bяк і відповідно. За рівняннями прямих aі bможна визначити координати напрямних векторів цих прямих – одержуємо і . Тоді для перпендикулярності прямих aі bнеобхідно і достатньо, щоб виконувалася умова перпендикулярності векторів і тобто, щоб скалярний добуток векторів і дорівнював нулю: .

Отже, aі bу прямокутній системі координат Oxyна площині має вигляд де і - напрямні вектори прямих aі bвідповідно.

Ця умова зручно використовувати, коли легко знаходяться координати напрямних векторів прямих, а також коли прямим aі bвідповідають канонічні рівняння прямої на площині або параметричні рівняння прямої на площині.

приклад.

У прямокутній системі координат Oxyзадані три точки. Чи перпендикулярні прямі АВі АС?

Рішення.

Вектори є напрямними векторами прямих АВі АС. Звернувшись до статті координати вектора за координатами точок його початку та кінця, обчислюємо . Вектори та перпендикулярні, так як . Таким чином, виконується необхідна та достатня умова перпендикулярності прямих АВі АС. Отже, прямі АВі АСперпендикулярні.

Відповідь:

так, прямі перпендикулярні.

приклад.

Чи є прямі та перпендикулярними?

Рішення.

Напрямний вектор прямий , а - напрямний вектор прямий . Обчислимо скалярний добуток векторів та: . Воно на відміну від нуля, отже, напрямні вектори прямих не перпендикулярні. Тобто не виконується умова перпендикулярності прямих, тому вихідні прямі не перпендикулярні.

Відповідь:

ні, прямі не перпендикулярні.

Аналогічно, необхідна та достатня умова перпендикулярності прямих aі bу прямокутній системі координат Oxyzу тривимірному просторі має вигляд , де і - напрямні вектори прямих aі bвідповідно.

приклад.

Чи перпендикулярні прямі, задані у прямокутній системі координат Oxyzу тривимірному просторі рівняннями і?

Рішення.

Числа, що стоять у знаменниках канонічних рівнянь прямої у просторі, є відповідними координатами напрямного вектора прямої. А координатами напрямного вектора прямої, яка задана параметричними рівняннями прямої просторі, є коефіцієнти при параметрі. Таким чином, та - напрямні вектори заданих прямих. З'ясуємо, чи перпендикулярні вони: . Оскільки скалярний добуток дорівнює нулю, ці вектори перпендикулярні. Отже, виконується умова перпендикулярності заданих прямих.

Відповідь:

прямі перпендикулярні.

Для перевірки перпендикулярності двох прямих на площині існують інші необхідні та достатні умови перпендикулярності.

Теорема.

Для перпендикулярності прямих aі bна площині необхідно і достатньо, щоб нормальний вектор прямий aбув перпендикулярний до нормального вектора прямої b.

Озвучена умова перпендикулярності прямих зручно використовувати, якщо за заданими рівняннями прямих легко знаходяться координати прямих векторних векторів. Цьому твердженню відповідає загальне рівняння прямого виду рівняння прямої у відрізках і рівняння прямої з кутовим коефіцієнтом.

приклад.

Переконайтеся, що прямі та перпендикулярні.

Рішення.

За заданими рівняннями прямих легко знайти координати нормальних векторів цих прямих. – нормальний вектор прямий . Перепишемо рівняння у вигляді , Звідки видно координати нормального вектора цієї прямої: .

Вектори і перпендикулярні, тому що їх скалярний добуток дорівнює нулю: . Таким чином, виконується необхідна та достатня умова перпендикулярності заданих прямих, тобто вони дійсно перпендикулярні.

Зокрема, якщо пряму aна площині визначає рівняння прямої з кутовим коефіцієнтом виду, а пряму b- виду, то нормальні вектори цих прямих мають координати і відповідно, а умова перпендикулярності цих прямих зводиться до наступного співвідношення між кутовими коефіцієнтами.

приклад.

Чи перпендикулярні прямі та ?

Рішення.

Кутовий коефіцієнт прямий дорівнює, а кутовий коефіцієнт прямий дорівнює. Добуток кутових коефіцієнтів дорівнює мінус одиниці, отже, прямі перпендикулярні.

Відповідь:

задані прямі перпендикулярні.

Можна озвучити ще одну умову перпендикулярності прямих на площині.

Теорема.

Для перпендикулярності прямих aі bна площині необхідно і достатньо, щоб напрямний вектор однієї прямої та нормальний вектор другої прямої були колінеарні.

Цією умовою, очевидно, зручно користуватися, коли легко знаходяться координати напрямного вектора однієї прямої і координати нормального вектора другої прямої, тобто коли одна пряма задана канонічним рівнянням або параметричними рівняннями прямої на площині, а друга - або загальним рівнянням прямої, або рівнянням прямої у відрізках, або рівнянням прямої з кутовим коефіцієнтом.

приклад.

Чи є прямі та перпендикулярними?

Рішення.

Очевидно, - нормальний вектор прямий, а - напрямний вектор прямий. Вектори і не колінеарні, тому що для них не виконується умова колінеарності двох векторів (не існує такого дійсного числа t, за якого ). Отже, задані прямі не є перпендикулярними.

Відповідь:

прямі не перпендикулярні.

21. Відстань від точки до прямої.

Відстань від точки до прямої визначається через відстань від точки до точки. Покажемо, як це робиться.

Нехай на площині або тривимірному просторі задана пряма aі крапка M 1, не лежачи на прямий a. Проведемо через точку M 1пряму b, перпендикулярну до прямої a. Позначимо точку перетину прямих aі bяк H 1. Відрізок M 1 H 1називається перпендикуляром, проведеним з точки M 1до прямої a.

Визначення.

Відстань від точки M 1до прямої a називають відстань між точками M 1і H 1.

Однак частіше зустрічається визначення відстані від точки до прямої, у якому фігурує довжина перпендикуляра.

Визначення.

Відстань від точки до прямої- Це довжина перпендикуляра, проведеного з цієї точки до цієї прямої.

Це визначення еквівалентне першому визначенню відстані від точки до прямої.

Зверніть увагу на те, що відстань від точки до прямої – це найменша відстань від цієї точки до точок заданої прямої. Покажемо це.

Візьмемо на прямий aточку Q, що не збігається з точкою M 1. Відрізок M 1 Qназивають похилій, проведеної з точки M 1до прямої a. Нам слід показати, що перпендикуляр, проведений з точки M 1до прямої a, менше будь-якої похилої, проведеної з точки M 1до прямої a. Це справді так: трикутник M 1 QH 1прямокутний з гіпотенузою M 1 Q, а довжина гіпотенузи завжди більша за довжину будь-якого з катетів, отже, .

22. Площина у просторі R3. Рівняння площини.

Площина в декартовій прямокутній системі координат може бути задана рівнянням, яке називається загальним рівняннямплощині.

Визначення.Вектор перпендикулярний площині і називається її нормальний вектор.

Якщо прямокутної системі координат відомі координати трьох точок , які не лежать на одній прямій, то рівняння площини записується у вигляді: .

Обчисливши цей визначник, отримаємо загальне рівняння площини.

приклад.Написати рівняння площині, що проходить через .

Рішення:

Рівняння площини: .

23. Дослідження загального рівняння площини.

Визначення 2. Будь-який вектор, перпендикулярний до площини, називається нормальним вектором цієї площини.

Якщо відома фіксована точка M 0 (x 0 , y 0 , z 0), що лежить у даній площині, і вектор , перпендикулярний даній площині, то рівняння площини, що проходить через точку M 0 (x 0 , y 0 , z 0), перпендикулярно вектору, має вигляд

A(x-x 0)+ B(y-y 0)+ C(z-z 0)= 0. (3.22)

Покажемо, що рівняння (3.22) є загальним рівнянням площини (3.21). Для цього розкриємо дужки та зберемо у дужки вільний член:

.Ax + By + Cz +(-Ax 0 - By -Cz 0)= 0

Позначивши D = -Ax 0 - By -Cz 0 , отримаємо рівняння Ax + By + Cz + D= 0.

Завдання 1.Скласти рівняння площини, що проходить через точку А, перпендикулярно вектору , якщо A(4, -3, 1), B(1, 2, 3).

Рішення.Знайдемо нормальний вектор площини:

Для знаходження рівняння площини використовуємо рівняння (3.22):

Відповідь: -3x + 5y + 2z + 25 = 0.

Завдання 2.Скласти рівняння площини, що проходить через точку M 0 (-1, 2, -1), перпендикулярно до осі OZ.

Рішення.Як нормальний вектор шуканої площини можна взяти будь-який вектор, що лежить на осі OZ, наприклад, тоді рівняння площини

Відповідь: z + 1 = 0.

24. Відстань від точки до площини.

Відстань від точки до площини визначається через відстань від точки до точки, одна з яких - задана точка, а інша - проекція заданої точки на задану площину.

Нехай у тривимірному просторі задана точка М 1і площину. Проведемо через точку М 1пряму aперпендикулярну до площини. Позначимо точку перетину прямої aі площині як H 1. Відрізок M 1 H 1називають перпендикуляром, опущеним з точки М 1на площину, а точку H 1 – основою перпендикуляра.

Визначення.

– це відстань від даної точки до основи перпендикуляра, проведеного із заданої точки до заданої площини.

Найчастіше зустрічається визначення відстань від точки до площини у такому вигляді.

Визначення.

Відстань від точки до площини- Це довжина перпендикуляра, опущеного із заданої точки до заданої площини.

Слід зазначити, що відстань від точки М 1до площини , визначене таким чином, є найменшою відстаней від заданої точки М 1до будь-якої точки площини. Справді, нехай точка H 2лежить у площині та відмінна від точки H 1. Очевидно, трикутник М 2 H 1 H 2є прямокутним, у ньому М 1 H 1- катет, а M 1 H 2- гіпотенуза, отже, . До речі, відрізок M 1 H 2називається похилій, проведеної з точки М 1до площини. Отже, перпендикуляр, опущений із заданої точки на задану площину, завжди менше похилої, проведеної з цієї точки до заданої площини.

Якщо пряма проходить через дві задані точки , то її рівняннязаписують у вигляді : .

Визначення.Вектор називається напрямнимвектор прямий, якщо він паралельний або належить їй.

приклад.Написати рівняння прямої, що проходить через дві задані точки .

Рішення: Використовуємо загальну формулу прямої, що проходить через дві задані точки: - канонічне рівняння прямої, що проходить через точки та . Вектор - напрямний вектор прямий.

26. Взаємне розташування прямих у просторі R3.

Перейдемо до варіантів взаємного розташування двох прямих у просторі.

По-перше, дві прямі можуть збігатися, тобто мати нескінченно багато загальних точок (принаймні дві спільні точки).

По-друге, дві прямі у просторі можуть перетинатися, тобто мати одну загальну точку. В цьому випадку ці дві прямі лежать у деякій площині тривимірного простору. Якщо дві прямі в просторі перетинаються, то ми приходимо до поняття кута між прямими, що перетинаються.

По-третє, дві прямі у просторі можуть бути паралельними. У цьому випадку вони лежать в одній площині та не мають спільних точок. Рекомендуємо до вивчення статті паралельні прямі, паралельність прямих.

Після того як ми дали визначення паралельних прямих у просторі, слід сказати вона правлячих векторах прямої лінії в силу їх важливості. Будь-який ненульовий вектор, що лежить на цій прямій або на прямій, яка паралельна даній, називатимемо напрямним вектором прямий. Напрямний вектор прямий часто використовується при вирішенні завдань, пов'язаних з прямою лінією в просторі.

Нарешті, дві прямі в тривимірному просторі можуть бути схрещуються. Дві прямі в просторі називаються такими, що схрещуються, якщо вони не лежать в одній площині. Таке взаємне розташування двох прямих у просторі приводить нас до поняття кута між прямими, що схрещуються.

Особливе практичне значення має випадок, коли кут між прямими, що перетинаються або схрещуються, в тривимірному просторі дорівнює дев'яноста градусам. Такі прямі називають перпендикулярними (дивіться статтю перпендикулярні до прямих, перпендикулярність до прямих).

27. Взаємне розташування прямої та площини у просторі R3.

Пряма може лежати на даній площині, бути паралельною даній площині або перетинати її в одній точці, див. наступні малюнки.

Якщо , то це означає, що . А таке можливе лише тоді, коли пряма лежить на площині або паралельна до неї. Якщо пряма лежить на площині, то будь-яка точка прямої є точкою площини і координати будь-якої точки прямої задовольняють рівняння площини. Тому достатньо перевірити, чи на площині лежить точка . Якщо , то точка – лежить на площині, а це означає, що й сама пряма лежить на площині.

Якщо , а , то точка на прямій не лежить на площині, а це означає, що пряма паралельна площині.

Теорему доведено.

У статті розглядається питання про перпендикулярні прямі на площині та тривимірному просторі. Визначення перпендикулярних прямих та їх позначення з наведеними прикладами докладно розберемо. Розглянемо умови застосування необхідної та достатньої умови перпендикулярності двох прямих та докладно розглянемо на прикладі.

Кут між прямими, що перетинаються, в просторі може бути прямим. Тоді кажуть, що ці прямі перпендикулярні. Коли кут між схрещуваними прямими прямими, тоді прямі також є перпендикулярними. Звідси випливає, що перпендикулярні прямі на площині, що перетинаються, а перпендикулярні прямі простори можуть бути перетинаються і схрещуються.

Тобто поняття «прямі a та b перпендикулярні» та «прямі b і a перпендикулярні» вважаються рівноправними. Звідси й узялося поняття взаємно перпендикулярних прямих. Узагальнивши сказане вище, розглянемо визначення.

Визначення 1

Дві прямі називають перпендикулярними, якщо кут при їхньому перетині дає 90 градусів.

Перпендикулярність позначається « ⊥ », а запис набуває вигляду a ⊥ b , що означає, прямий a перпендикулярний до прямої b .

Наприклад, перпендикулярними прямими на площині можуть бути сторони квадрата із загальною вершиною. У тривимірному просторі прямі O x , O z , O y перпендикулярні попарно: O x і O z , O x і O y , O y і O z .

Перпендикулярність прямих – умови перпендикулярності

Властивості перпендикулярності необхідно знати, оскільки більшість завдань зводиться до перевірки для подальшого рішення. Бувають випадки, коли про перпендикулярність йдеться ще за умови завдання або коли необхідно скористатися доказом. Для того щоб довести перпендикулярність достатньо, щоб кут між прямими був прямим.

Для того, щоб визначити їхню перпендикулярність при відомих рівняннях прямокутної системи координат, необхідно застосувати необхідну і достатню умову перпендикулярності прямих. Розглянемо формулювання.

Теорема 1

Для того, щоб прямі a і b були перпендикулярними, необхідно і достатньо, щоб напрямний вектор прямий мав перпендикулярність щодо напрямного вектора заданої прямої b .

Сам доказ ґрунтується на визначенні напрямного вектора прямої та на визначенні перпендикулярності прямих.

Доказ 1

Нехай введена прямокутна декартова система координат Ох у заданими рівняннями прямої на площині, які визначають прямі a і b . Напрямні вектори прямих a і b позначимо a → b → . З рівняння прямих a і b необхідною та достатньою умовою є перпендикулярність векторів a → і b → . Це можливо тільки при скалярному добутку векторів a → = (a x , a y) і b → = (b x , b y) рівному нулю, а запис має вигляд a → b → = a x b + a y b y = 0 . Отримаємо, що необхідною і достатньою умовою перпендикулярності прямих a і b , що знаходяться в прямокутній системі координат О х у на площині, є a → , b = a x b + a y b y = 0 , де a = (a x , a y) і b → = b x , b y це напрямні вектори прямих a і b .

Умова застосовна, коли необхідно знайти координати напрямних векторів або за наявності канонічних або параметричних рівнянь прямих на заданих площині прямих a і b .

Приклад 1

Задані три точки A (8, 6), B (6, 3), C (2, 10) у прямокутній системі координат О х у. Визначити, прямі АВ і АС перпендикулярні чи ні.

Рішення

Прямі АВ і АС мають напрямні вектори A B → і A C → відповідно. Для початку обчислимо A B → = (- 2, - 3), A C → = (-6, 4). Отримаємо, що вектори A B → і A C → перпендикулярні властивості про скалярний добуток векторів, що дорівнює нулю.

A B → , A C → = (-2) · (-6) + (-3) · 4 = 0

Очевидно, що необхідну і достатню умову можна здійснити, отже, АВ і АС перпендикулярні.

Відповідь:прямі перпендикулярні.

Приклад 2

Визначити, задані прямі x - 1 2 = y - 7 3 і x = 1 + λ y = 2 - 2 · λ перпендикулярні чи ні.

Рішення

a → = (2 , 3) ​​є напрямним вектором заданої прямої x - 1 2 = y - 7 3

b → = (1 , - 2) є напрямним вектором прямий x = 1 + λ y = 2 - 2 · λ.

Перейдемо до обчислення скалярного добутку векторів a → та b →. Вираз буде записано:

a → , b → = 2 · 1 + 3 · - 2 = 2 - 6 ≠ 0

Результат твору не дорівнює нулю, можна дійти невтішного висновку, що вектори не перпендикулярні, отже і прямі також перпендикулярні.

Відповідь:прямі не перпендикулярні.

Необхідна і достатня умова перпендикулярності прямих a і b застосовується для тривимірного простору, записується у вигляді a → , b → = a x · b x + a y · b y a z · b z = 0 , де a = (a x , a y , a z) і b → = (b x , b y , b z) є напрямними векторами прямих a і b.

Приклад 3

Перевірити перпендикулярність прямих у прямокутній системі координат тривимірного простору, задані рівняннями x 2 = y - 1 = z + 1 0 та x = λ y = 1 + 2 · λ z = 4 · λ

Рішення

Знаменники з канонічних рівнянь прямих вважаються координатами напрямного вектора прямої. Координати напрямного вектора з параметричного рівняння – коефіцієнти. Звідси випливає, що a → = (2, - 1, 0) і b → = (1, 2, 4) є напрямними векторами заданих прямих. Для виявлення їхньої перпендикулярності знайдемо скалярний добуток векторів.

Вираз набуде вигляду a → , b → = 2 · 1 + (- 1) · 2 + 0 · 4 = 0 .

Вектори перпендикулярні, оскільки добуток дорівнює нулю. Необхідна і достатня умова виконана, отже прямі перпендикулярні.

Відповідь:прямі перпендикулярні.

Перевірка перпендикулярності може проводитись, виходячи з інших необхідних та достатніх умов перпендикулярності.

Теорема 2

Прямі a і b на площині вважаються перпендикулярними при перпендикулярності нормального вектора прямої a з вектором b це і є необхідна і достатня умова.

Доказ 2

Ця умова застосовна, коли рівняння прямих дають швидке знаходження координат нормальних векторів заданих прямих. Тобто за наявності загального рівняння прямої виду A x + B y + C = 0 рівняння прямої у відрізках виду x a + y b = 1 рівняння прямої з кутовим коефіцієнтом виду y = k x + b координати векторів можна знайти.

Приклад 4

З'ясувати, чи перпендикулярні прямі 3 x - y + 2 = 0 і x 3 2 + y 1 2 = 1 .

Рішення

Виходячи із їх рівнянь, необхідно знайти координати нормальних векторів прямих. Отримаємо, що n α → = (3 - 1) - це нормальний вектор для прямої 3 x - y + 2 = 0 .

Спростимо рівняння x 3 2 + y 1 2 = 1 до виду 23 x + 2 y - 1 = 0 . Тепер чітко видно координати нормального вектора, які запишемо у такій формі n b → = 2 3 , 2 .

Вектори n a → = (3 , - 1) і n b → = 2 3 , 2 будуть перпендикулярними, оскільки їх скалярний добуток дасть у результаті значення 0 . Отримаємо n a → , n b → = 3 · 2 3 + (-1) · 2 = 0 .

Необхідна та достатня умова була виконана.

Відповідь:прямі перпендикулярні.

Коли пряма a на площині визначена за допомогою рівняння з кутовим коефіцієнтом y = k 1 x + b 1 , а пряма b - y = k 2 x + b 2 звідси випливає, що нормальні вектори матимуть координати (k 1 , - 1) і (k 2 - 1) . Сама умова перпендикулярності зводиться до k 1 · k 2 + (- 1) · (- 1) = 0 ⇔ k 1 · k 2 = - 1 .

Приклад 5

З'ясувати, чи перпендикулярні прямі y = - 3 7 x та y = 7 3 x - 1 2 .

Рішення

Пряма y = - 3 7 x має кутовий коефіцієнт, що дорівнює - 3 7 , а пряма y = 7 3 x - 1 2 - 7 3 .

Добуток кутових коефіцієнтів дає значення - 1, - 3 7 · 7 3 = - 1, тобто прямі є перпендикулярними.

Відповідь:задані прямі перпендикулярні.

Є ще одна умова, що використовується визначення перпендикулярності прямих на площині.

Теорема 3

Для перпендикулярності прямих a і b на площині необхідною і достатньою умовою є колінеарність напрямного вектора однієї з прямих з нормальним вектором другої прямої.

Доказ 3

Умова застосовна, коли є можливість знаходження напрямного вектора однієї прямої та координат нормального вектора інший. Інакше висловлюючись, одна пряма задається канонічним чи параметричним рівнянням, іншу загальним рівнянням прямої, рівнянням у відрізках чи рівнянням прямої з кутовим коефіцієнтом.

Приклад 6

Визначити, чи задані прямі x - y - 1 = 0 і x 0 = y - 4 2 перпендикулярними.

Рішення

Виходить, що нормальний вектор прямий x - y - 1 = 0 має координати n a → = (1 , - 1) , а b → = (0 , 2) - напрямний вектор прямий x 0 = y - 4 2 .

Звідси видно, що вектори n a → = (1 , - 1) і b → = (0 , 2) не є колінеарними, тому що умова колінеарності не виконується. Не існує такого числа t, щоб виконувалася рівність n a → = t · b →. Звідси висновок, що прямі є перпендикулярними.

Відповідь:прямі не перпендикулярні.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

У цій статті докладно розглянемо на площині та у тривимірному просторі. Почнемо з визначення перпендикулярних прямих, покажемо позначення та наведемо приклади. Після цього наведемо необхідну та достатню умову перпендикулярності двох прямих і детально розберемо розв'язання характерних завдань.

Навігація на сторінці.

Перпендикулярні прямі основні відомості.

приклад.

У прямокутній системі координат Oxy задані три точки. Чи перпендикулярні прямі АВ та АС?

Рішення.

Вектори є напрямними векторами прямих АВ і АС . Звернувшись до статті, обчислюємо . Вектори та перпендикулярні, так як . Таким чином, виконується необхідна та достатня умова перпендикулярності прямих АВ та АС. Отже, прямі АВ та АС перпендикулярні.

Відповідь:

Так, прямі перпендикулярні.

приклад.

Чи є прямі та перпендикулярними?

Рішення.

Напрямний вектор прямий , а - напрямний вектор прямий . Обчислимо скалярний добуток векторів та: . Воно на відміну від нуля, отже, напрямні вектори прямих не перпендикулярні. Тобто не виконується умова перпендикулярності прямих, тому вихідні прямі не перпендикулярні.

Відповідь:

Ні, прямі не перпендикулярні.

Аналогічно, необхідна та достатня умова перпендикулярності прямих a і b у прямокутній системі координат Oxyz у тривимірному просторі має вигляд , де і - Спрямовують вектори прямих a і b відповідно.

приклад.

Чи перпендикулярні прямі, задані у прямокутній системі координат Oxyz у тривимірному просторі рівняннями і?

Рішення.

Числа, що стоять у знаменниках канонічних рівнянь прямої в просторі є відповідними координатами напрямного вектора прямої. А координатами напрямного вектора прямої, яка задана параметричними рівняннями прямої в просторі є коефіцієнти при параметрі. Таким чином, та - напрямні вектори заданих прямих. З'ясуємо, чи перпендикулярні вони: . Оскільки скалярний добуток дорівнює нулю, ці вектори перпендикулярні. Отже, виконується умова перпендикулярності заданих прямих.

Відповідь:

Прямі перпендикулярні.

Для перевірки перпендикулярності двох прямих на площині існують інші необхідні та достатні умови перпендикулярності.

Теорема.

Для перпендикулярності прямих a і b на площині необхідно і достатньо, щоб нормальний вектор прямий був перпендикулярний нормальному вектору прямий b .

Озвучена умова перпендикулярності прямих зручно використовувати, якщо за заданими рівняннями прямих легко знаходяться координати прямих векторних векторів. Цьому твердженню відповідає загальне рівняння прямого виду рівняння прямої у відрізках і рівняння прямої з кутовим коефіцієнтом.

приклад.

Переконайтеся, що прямі та перпендикулярні.

Рішення.

За заданими рівняннями прямих легко знайти координати нормальних векторів цих прямих. – нормальний вектор прямий . Перепишемо рівняння у вигляді , Звідки видно координати нормального вектора цієї прямої: .

Вектори і перпендикулярні, тому що їх скалярний добуток дорівнює нулю: . Таким чином, виконується необхідна та достатня умова перпендикулярності заданих прямих, тобто вони дійсно перпендикулярні.

Зокрема, якщо пряму a на площині визначає рівняння прямої з кутовим коефіцієнтом виду, а пряму b – виду, то нормальні вектори цих прямих мають координати і відповідно, а умова перпендикулярності цих прямих зводиться до наступного співвідношення між кутовими коефіцієнтами.

Теорема.З точки, що не лежить на прямій, можна провести перпендикуляр до цієї прямої.

Доведення.Нехай A – точка, що не лежить на цій прямій a (рис. 56, а). Доведемо, що з точки A можна провести перпендикуляр прямої a. Подумки перегнемо площину прямою a (рис. 56, б) так, щоб напівплощина з кордоном a, що містить точку A, наклалася на іншу напівплощину. При цьому точка A накладеться на деяку точку. Позначимо її літерою B. Розігнемо площину і проведемо через точки A та Bпряму.

Нехай H – точка перетину прямих AB та a (рис. 56, в). При повторному перегинанні площини по прямій точці H залишиться на місці. Тому промінь HA накладеться на промінь HB і, отже, кут 1 сумісний з кутом 2. Таким чином, ∠1 = ∠2. Оскільки кути 1 і 2 – суміжні, їх сума дорівнює 180°, тому кожен із новачків – прямий. Отже, відрізок AH перпендикуляр до прямої a. Теорему доведено.

26. Доведіть теорему про єдиність перпендикуляра до прямої. (Рис.57 у підручнику)

Теорема. З точки, що не лежить на прямій, не можна провести два перпендикуляри до цієї прямої.

Доведення.Нехай A – точка, що не лежить на цій прямій a (див. рис. 56, а). Доведемо, що з точки Aне можна провести два перпендикуляри до прямої a. Припустимо, що з точки A можна провести два перпендикуляри AH та AK до прямої a (рис. 57). Подумки перегнемо площину по прямій a так, щоб напівплощина з кордоном a, що містить точку A, наклалася на іншу напівплощину. При перегинанні точки H та K залишаються на місці, точка A накладається на деяку точку. Позначимо її літерою B. У цьому відрізки AH і AK накладаються на відрізки BH і BK.

Кути AHB і AKB – розгорнуті, оскільки кожен із них дорівнює сумі двох прямих кутів. Тому точки A, Hі B лежать на одній прямій і точки A, K і B лежать на одній прямій.

Таким чином ми отримали, що через точки A і B проходять дві прямі AH і AK. Але цього може бути. Отже, наше припущення є невірним, а значить, з точки A не можна провести два перпендикуляри до прямої a. Теорему доведено.

http://mthm.ru/geometry7/perpendicular