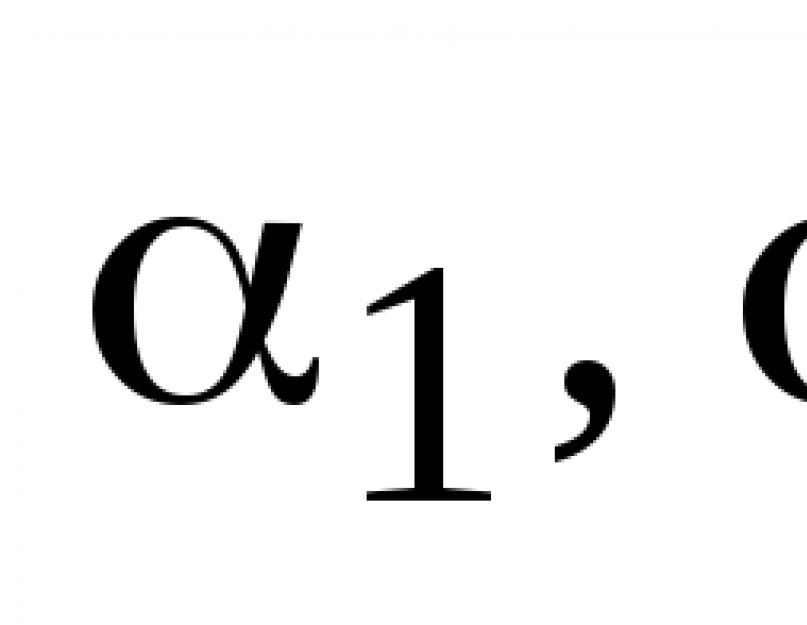Algebra va geometriya bo'yicha ma'ruzalar. Semestr 1

Ma’ruza 9. Vektor fazoning asoslari.

Qisqa muddatli: vektor sistemasi, vektor sistemaning chiziqli birikmasi, vektor sistemasining chiziqli birikmasi koeffitsientlari, to‘g‘ri chiziqdagi asos, maydon va fazo, chiziq, maydon va fazodagi vektor fazolarning o‘lchamlari, vektorga ko‘ra parchalanishi. bazis, bazis bo'yicha vektorning koordinatalari, rashk haqida teorema ikki vektor, koordinata yozuvidagi vektorlar ustida chiziqli amallar, vektorlarning ortonormal uchligi, vektorlarning o'ng va chap uchligi, ortonormal asos, vektor algebrasining bosh teoremasi.

9-bob. Vektor fazosining asoslari va vektorning bazis ortidagi parchalanishi.

1-band. Baza tekis chiziqda, tekis yuzada va kosmosda.

Viznachennya. Qanday bo'lmasin, cheksiz vektorlar vektorlar tizimi deb ataladi.

Viznachennya. Viraz, de
vektor sistemaning chiziqli birikmasi deyiladi
, va raqamlar
chiziqli birikma koeffitsientlari deyiladi.

L, P va S - to'g'ri bo'lsin, nuqtaning maydoni va fazosi parallel va
. Todi
- L to'g'ri chiziqda, P tekislikda va S fazoda to'g'ridan-to'g'ri kesmalar sifatida vektorlarning vektor fazolari izchil.

nolga teng bo'lmagan vektor deb ataladi
, keyin. har qanday nolga teng bo'lmagan kolinear vektor L bo'lsin:
і
.

Asosga tayinlangan
:
- Asos
.

Viznachennya. Vektor fazosining asosi
fazoda kollinear bo'lmagan vektorlar juftligi tartiblanganligi deyiladi
.

, de
,
- Asos
.

Viznachennya. Vektor fazosining asosi
fazoda uchta tekis bo'lmagan vektorlar tartiblanganda (bir tekislikda yotmaslik uchun) deyiladi.
.

- Asos
.

Hurmat. Vektor fazosining asosi nol vektorni almashtira olmaydi: fazoda
sahna ortida, ochiq maydonda
koinotda ikkita vektor kolinear bo'ladi, go'yo ulardan biri nolga teng bo'ladi
uchta vektor koplanar bo'ladi, shuning uchun ular bir xil tekislikda yotadi, go'yo uchta vektordan biri nolga teng bo'ladi.

2-band. Baza asosida vektorni joylashtirish.

Viznachennya. Qani ketdik - etarli vektor;
- Juda vektorlar tizimi. Rashk qanday tugaydi

vektorga o'xshaydi tasvirlar vektor tizimlarining chiziqli birikmasi kabi ko'rinadi. Vektorlar sistemasi berilgan
ê vektor fazosining asosi, keyin tenglik (1) vektorning parchalanishi deyiladi asosida
. Chiziqli birikma koeffitsientlari
vektorning koordinatalari shu tarzda deyiladi asosga
.

Teorema. (Baza ortida vektorlarning parchalanishi haqida.)

Vektor fazoning har qanday vektorini uning asosiga bitta usulda ajratish mumkin.

Tugallandi. 1) L to'g'ri chiziqdan (yoki butun narsadan) qanoatlansin.
- Asos
. Keling, juda yaxshi vektorni olaylik
. Xo'sh, vektorlar qanchalik xafa bo'lishadi і Kolinear bir va bir xil va to'g'ri L, keyin
. Ikki vektorning kolinearligi haqidagi tezlik teoremasi. Shunday ekan
, keyin bunday raqam bo'ladi
, nima
Shunday qilib, biz vektorni o'zimiz parchaladik asosida
vektor maydoni
.

Endi biz bunday tartibning birligini ko'rsatamiz. Qabul qilinmaydi. Keling, ikkita buklangan vektorga ega bo'laylik asosida
vektor maydoni
:

і
, de
. Todi
va vikoristik taqsimot qonuni rad etiladi:

Shunday ekan
, keyin qolgan g'ayrat bilan u oqadi
, Ch.t.d.

2) Endi u etarlicha tekis bo'lsin
- Asos
. Qani ketdik
maydonning qo'shimcha vektori. Biz uchta vektorni bitta tekislikning istalgan nuqtasiga qo'shamiz. Keling, 4 to'g'ri qolaylik. Keling, to'g'ri boraylik , qaysi biri ustida vektor yotadi bevosita
, qaysi biri ustida vektor yotadi . Vektorning oxiri orqali vektorga to'g'ridan-to'g'ri parallel chizish í to'g'ridan-to'g'ri vektorga parallel . 4 ta to'g'ri chiziq parallelogrammlarda osilgan. quyida rasm. 3. Paralelogramma qoidasiga rioya qilish
, і
,
,
- Asos ,
- Asos
.

Endi, bu dalilning birinchi qismini tugatgandan so'ng, bunday raqamlar mavjud
, nima

і
. Yulduzlar aniq:

va asos yaratish imkoniyatiga erishildi.

Endi biz parchalanishning birligini asos bilan ko'rsatamiz. Qabul qilinmaydi. Keling, ikkita buklangan vektorga ega bo'laylik asosida
vektor maydoni
:
і
. Rashkni olib tashlash mumkin

Keyingi yulduzlar
. Yakshcho
, Bu
, Va shundan beri
, Bu
va belgilangan darajadagi koeffitsientlar:
,
. Endi boraylik
. Todi
, de
. Ikki vektorning kolinearligi haqidagi teoremadan kelib chiqib, bundan kelib chiqadi
. Aqlni chalg'itadigan teoremalar paydo bo'ldi. Otje,
і
, Ch.t.d.

3) Qo'yib yuboring
- Asos
va meni qo'yib yuboring
chiroyli vektor. Keling, shunday vaqt o'tkazaylik.

Biz uchta asosiy vektorni o'z ichiga olamiz
ta vektor Bir nuqtadan 6 ta tekislik bo'ladi: bazis vektorlari yotadigan tekislik
, maydon
o'sha hudud
; vektorning oxirigacha bo'lgan masofa Keling, uchta tekislikni ehtiyotkorlik bilan yaratib, parallel ravishda uchta tekislikni chizamiz. Parallelepipedda 6 ta samolyot bor:

Vektorlarni katlama qoidasi hasadni anglatadi:

. (1)

Har kuni
. Ikki vektorning kolinearligi haqidagi teoremaga asoslanib, asosiy son
, Xo'sh
. Xuddi shunday,
і
, de
. Endi, tengliklarni (1) o'rniga, biz olib tashlashimiz mumkin:

va asos yaratish imkoniyatiga erishildi.

Keling, bunday tartibning birligini namoyish qilaylik. Qabul qilinmaydi. Keling, ikkita buklangan vektorga ega bo'laylik asosida
:

I. Todi

Azizim, miya vektorining orqasida nima bor
koplanar bo'lmagan, shuning uchun ular juft-kolinear bo'lmagan hidlaydi.

Ikkita mumkin bo'lgan stsenariy mavjud:
yoki yana
.

a) qo'yib yuboring
, Todi g'ayrat bilan (3) qichqiradi:

. (4)

Rashk bilan (4) vektor sifatida porlaydi asosiga ko'ra parchalanadi
, keyin. vektor vektor kvadratiga yaqin joyda yoting
va, shuningdek, vektorlar
koplanar, bu ongni kuchaytiradi.

b) tushishni yo'qotish
, keyin.
. Tenglik bilan Todi (3) olib tashlanishi mumkin yoki

Shunday ekan
- vektorlar fazosining asosi tekislikda yotadi va biz allaqachon maydon vektorlari asosiga ko'ra parchalanish birligini keltirdik, keyin (5) tenglikdan kelib chiqadiki,
і
, Ch.t.d.

Teorema isbotlangan.

Tekshiruv.

1) Vektor fazoda anonim vektorlar o'rtasida o'zaro bir ma'noli munosabat mavjud
va hech qanday faol raqamlarsiz R.

2) Vektor fazoda anonim vektorlar o'rtasida o'zaro bir ma'noli muvofiqlik mavjud
va kartezyen kvadrat

3) Vektor fazoda anonim vektorlar o'rtasida o'zaro bir ma'noli muvofiqlik mavjud
va kartezian kubi
haqiqiy sonlar ko'paytmalari R.

Tugallandi. Biz uchinchi nuqtaga yetib keldik. Birinchi ikkitasi xuddi shunday tarzda ko'rib chiqiladi.

Kosmosda tanlang va tuzating
qanday asosda
va displey boshqariladi
keyingi qoidaga muvofiq:

tobto. Teri vektoriga koordinatalar to'plamining tartiblash turi tayinlanadi.

Ruxsat etilgan asosda vektor bitta koordinata to'plamini o'z ichiga olganligi sababli, (6) qoidada ko'rsatilgan ko'rinish tasvirlarda samarali bo'ladi.

Teoremaning isboti shuni ko'rsatadiki, turli vektorlar bir xil asosga asoslangan turli koordinatalarga ega. Displey (6) ta'sir yo'q degan ma'noni anglatadi.

Qani ketdik
Faol raqamlarni terishning ko'proq tartibi.

Keling, vektorni ko'rib chiqaylik
. Bu vektor koordinatalariga ega
. Xo'sh, tasvir (6) shubhasizdir.

Tasvir ham faol, ham sur'aktiv va samarasiz. o'zaro bir ma'noli va boshqalar.

Tergov yakunlandi.

Teorema. (Ikki vektorning tengligi haqida.)

Ikki vektor teng bo'ladi, agar ularning koordinatalari bir xil asosga teng bo'lsa.

Dalil dastlabki tergovdan darhol paydo bo'ladi.

3-band. Vektor fazosining o'lchami.

Viznachennya. Vektor fazo asosidagi vektorlar soni uning o'lchami deyiladi.

Belgilangan:
- Vektor fazosining kattaligi V.

Shunday qilib, bu va oldingi qiymatlarga o'xshashlik, biz aytishimiz mumkin:

1)
- L chiziqli vektorlarning vektor fazosi.

- Asos
,
,
,
- Layout vektori
asosida
,
- vektor koordinatasi asosga
.

2)
- R maydoni vektorlarining vektor fazosi.

- Asos
,
,
,
- Layout vektori
asosida
,
- vektor koordinatalari asosga
.

3)
– S fazo nuqtasidagi vektorlarning vektor fazosi.

- Asos
,
,
- Layout vektori
asosida
,
- vektor koordinatalari asosga
.

Hurmat. Yakshcho
, Bu
va siz asosni tanlashingiz mumkin
bo'sh joy
Xo'sh
- Asos
і
- Asos
. Todi
, і
, .

Shunday qilib, L to'g'ri chiziqning istalgan vektorini, P maydoni yoki S fazosini bazisga ko'ra ajratish mumkin
:

Uchrashuv. Vektorlarning tengligi haqidagi teorema tufayli biz haqiqiy sonlarning tartiblangan uchligidan istalgan vektorni aniqlab, quyidagicha yozishimiz mumkin:

Bu, agar asos bo'lsa, bu holda kamroq ahamiyatga ega bo'lishi mumkin
fiksatsiyalar va chalkashlik xavfi yo'q.

Viznachennya. Vektorni tartiblangan haqiqiy sonlar uchligi shaklida yozish vektorni yozish koordinata shakli deyiladi:
.

4-band. Koordinatalar ko'rinishidagi vektorlar bilan chiziqli amallar.

Qani ketdik
- makon asosi
і
- ikkita qo'shimcha vektor. Qani ketdik
і
– bu vektorlarni koordinata shaklida qayd etish. Oldinga, oldinga,
- Juda samarali raqam. Bu nomlar bir xil teoremaga ega.

Teorema. (Koordinata shaklidagi vektorlar bilan chiziqli amallar haqida.)

2)
.

Boshqacha qilib aytganda, ikkita vektorni qo'shish uchun ularning koordinatalarini qo'shish kerak, vektorni songa ko'paytirish uchun esa berilgan vektorning koordinatalarini berilgan songa ko'paytirish kerak.

Tugallandi. Mental teoremaga amal qilgan holda, vektorlarni katlama va vektorni songa ko'paytirish amallari asosidagi vektor fazosining vikoristik aksiomalari ayiriladi:

Yulduz qichqirmoqda.

Xuddi shu narsa hasadga ham tegishli.

Teorema isbotlangan.

5-band. Ortogonal vektorlar. Ortonormal asos.

Viznachennya. Ikki vektor ortogonal deb ataladi, chunki ular orasidagi yo'l to'g'ridan-to'g'ri yo'lga o'xshaydi.
.

Belgilangan:
- Vektorlar і ortogonal

Viznachennya. Uch vektor
vektorlar bir-biriga juft ortogonal bo'lgani uchun ortogonal deyiladi.
,
.

Viznachennya. Uch vektor
ortogonal bo'lgani uchun va barcha vektorlar birliklarga ega bo'lmaguncha ortonormal deyiladi:
.

Hurmat. Qiymat shundan kelib chiqadiki, vektorlarning uchligi ortogonal va shuning uchun ortonormal va koplanar emas.

Viznachennya. Vektorlarning koplanar bo'lmagan triosi tartiblangan
, xuddi shu nuqtada joylashgan, o'ng (o'ngga yo'naltirilgan) deb ataladi, chunki u uchinchi vektorning oxiridan keladi. birinchi ikkita vektor yotadigan maydonga і , birinchi vektorning eng qisqa aylanishi boshqasiga yubiley o'qi qarshisida paydo bo'ladi. Boshqa holatda, uchta vektor chap (chapga yo'naltirilgan) deb ataladi.

Bu erda, 6-rasmda, o'ng uchta vektor ko'rsatilgan
. Keyingi 7-rasmda chap uchta vektor ko'rsatilgan
:

Viznachennya. Asos
vektor maydoni
ortonormalizatsiya deyiladi, chunki
Vektorlar uchligi ortonormaldir.

Uchrashuv. Bizda to'g'ri ortonormal asos bor.
div. kichiklarga hujum qilish.

Vektorlarning chiziqliligi va chiziqliligi.
Vektor asoslari. Afina koordinata tizimi

Sinfda shokoladlar juda ko'p bo'ladi va teri konditsioneri bugun bir juft qizilmiya oladi - chiziqli algebra bilan analitik geometriya. Ushbu maqolada asosiy matematikaning ikkita bo'limi yo'q qilinadi va biz ularning bir kuyishda qanday yashashiga hayron bo'lamiz. Tanaffus qiling va "Twix" o'ynang! ...mlynets, yaxshi va nísenítnitsa superechok. Agar xohlasam, taslim bo'lmayman, ijobiy munosabat bilan boshlashga tayyorman.

Vektorlarning chiziqli joylashuvi, vektorlarning chiziqli mustaqilligi, vektorlar asosi Ikkala atama ham nafaqat geometrik talqinga, balki, birinchi navbatda, algebraik ma'noga ega bo'lishi mumkin. "Vektor" ning o'zini chiziqli algebra nuqtai nazaridan tushungan holda, u biz tekislikda yoki kosmosda tasvirlashimiz mumkin bo'lgan bir xil "asosiy" vektor emas. Dalil izlashning hojati yo'q, shunchaki penta-dunyoning vektorini chizishga harakat qiling. . Yoki kuting, men Gismeteoga bordim: - harorat va atmosfera bosimi bir xil. Ko't, albatta, vektor fazosidagi hokimiyat nuqtai nazaridan noto'g'ri, ammo hech kim bu parametrlarni vektor bilan rasmiylashtirish bilan bezovta qilmaydi. Kuz Dihana.

Yo'q, men sizni nazariya, chiziqli vektor bo'shliqlari bilan jalb qilmoqchi emasman, maqsad shuki tushunish teoremaning ma'nosi. Algebra nuqtai nazaridan barcha vektorlarga yangi atamalar (chiziqlilik, mustaqillik, chiziqli birikma, bazis va boshqalar) qo'llaniladi, ammo ilovalar geometrik bo'ladi. Shunday qilib, hamma narsa oddiy, mavjud va shaxsan. Analitik geometriya topshirig'iga qo'shimcha ravishda algebra topshiriqlarining turlarini ko'rib chiqamiz. Materialni o'zlashtirish uchun darslar bilan tanishish muhimdir Dummies uchun vektorlarі Qiymatni qanday hisoblaysiz?

Hudud vektorlarining chiziqliligi va mustaqilligi.
Tekislik asosi va affin koordinatalar sistemasi

Keling, kompyuter stolining sirtini ko'rib chiqaylik (faqat stol, choyshablar, choyshablar, stendlar, sizga mos keladigan narsa). Zavodannya hujumda qoladi:

1) Vibratsiyali asos tekisligi. Taxminan aytganda, ustunning uzunligi va kengligi bor, shuning uchun asos yaratish uchun ikkita vektor kerakligi intuitiv ravishda tushunildi. Bitta vektor etarli emas, uchta vektor chiqindidir.

2) Tanlangan asosga asoslanadi koordinatalar tizimini kiriting(koordinatalar panjarasi) jadvaldagi barcha ob'ektlarga koordinatalarni belgilash uchun.

Hayron bo'lmang, tushuntirish darhol barmoqlaringizda bo'ladi. Bundan tashqari, sizniki. Mehribon bo'ling, joy chap qo'lning vulgar barmog'i xonaning chetiga, shunda siz monitorga hayron bo'lasiz. Bu vektor bo'ladi. Endi joy o'ng qo'lning kichik barmog'i stolning chetida xuddi shunday - to'g'ridan-to'g'ri monitor ekraniga tushishi uchun. Bu vektor bo'ladi. Tabassum qiling, siz ajoyib ko'rinasiz! Vektorlar haqida nima deya olasiz? Dani vektorlari kolinear, bu degani chiziqli birin-ketin paydo bo'ladi:
, yaxshi, aslida: , de – deyake soni, vydmínne vyd nol.

Ushbu harakatning rasmini darsda ko'rishingiz mumkin Dummies uchun vektorlar Bu erda men vektorni songa ko'paytirish qoidasini tushuntirdim.

Qanday qilib barmoqlaringiz kompyuter stolining yuzasiga asosni o'rnatadi? Shubhasiz, yo'q. Kollinear vektorlar bu erda va u erda narxni oshiradi yolg'iz tekis, sirt esa eniga teng.

Bular vektorlar deyiladi chiziqli yolg'on.

Dovidka: "Chiziqli", "chiziqli" so'zlari matematik tenglamalarda kvadratlar, kublar, boshqa qadamlar, logarifmlar, sinuslar va boshqalar mavjud emasligini anglatadi. Faqat chiziqli (1-bosqich) ifodalar va joylashtirishlar.

Ikki vektor tekisligi chiziqli konlar Bu va faqat bu, agar ular kolinear bo'lsa.

Barmoqlaringizni stol ustiga bog'lang, shunda ular o'rtasida 0 dan 180 darajagacha farq bo'ladi. Ikki vektor tekisligichiziqli Yo'q u yoki bu holatda konlar, chunki hid kolinear emas. Xo'sh, asos olib tashlandi. Turli dovjinlarning perpendikulyar bo'lmagan vektorlari bilan Wijshov asosini "o'rish" haqida tashvishlanishning hojati yo'q. Biz uchun bu maqsadda nafaqat 90 daraja, balki yagona, teng vektorlar ham mavjud emasligi biz uchun muhimdir.

Nima bo'lsa ham maydon vektori bir martabada asosiga ko'ra ajratiladi:
, de-operatsion raqamlar. Raqamlarni nomlang vektor koordinatalari qanday asosda.

Demak, shunday ko'rinadi vektortomoshabinning qarashlari chiziqli birikma bazis vektorlari. Buni ular viraz deb atashadi ochiladigan vektorasosida yoki yana chiziqli birikma asosiy vektorlar.

Masalan, dekompozitsiyalar vektori tekislikning ortonormal asosi orqasida, deb aytishimiz mumkin va tasvirlar vektorlarning chiziqli birikmasi ko'rinishiga ega ekanligini aytishimiz mumkin.

Menga shakllantirishga ruxsat bering asos uchun qiymat rasmiy ravishda: Hududning asosi bir juft chiziqli mustaqil (kollinear bo'lmagan) vektorlar deyiladi, , qachon nima bo'lishi mumkin Maydon vektori bazis vektorlarining chiziqli birikmasidir.

Haqiqiy ahamiyatga ega bo'lgan moment - bu vektorlarning olinganligi kuylash tartibida. Basisi - bu ikkita mutlaqo boshqa asoslar! Chap qo'lingizning kichik barmog'ini o'ng qo'lingizning kichik barmog'i bilan almashtira olmaysiz.

Biz asosni saralab oldik, lekin kompyuter jadvalidagi har bir ob'ektga koordinatalar panjarasini o'rnatish va koordinatalarni belgilash etarli emas. Nega yetarli emas? Vektorlar erkin va butun sirt bo'ylab aylanib yuradilar. Xo'sh, dam olish kunlaridan keyin yo'qotgan stoldagi bu kichik shafqatsiz nuqtalarning koordinatalarini qanday berishimiz mumkin? Kerakli mos yozuvlar nuqtasi. Va bunday mos yozuvlar nuqtasi hamma uchun ma'lum bo'lgan nuqta - koordinatalarning boshlanishi. Keling, koordinatalar tizimini ko'rib chiqaylik:

Men "maktab" tashkilotidan boshlayman. Kirish darsida allaqachon Dummies uchun vektorlar Men to'g'ri chiziqli koordinatalar tizimi va ortonormal asos o'rtasidagi farqlarni ko'rdim. Aksning standart rasmi:

Haqida gapirganda to'g'ri chiziqli koordinatalar tizimi, keyin ko'pincha koordinatalar, koordinata o'qlari va o'qlar bo'ylab masshtab ko'rinadi. Qidiruv tizimida "to'g'ridan-to'g'ri koordinatalar tizimi" deb yozib ko'ring, shunda siz 5-6-sinfdan bilgan koordinata o'qlari va nuqtalarni tekislikda qanday joylashtirish haqida ko'p narsalarni bilib olishingizni ko'rasiz.

Boshqa tomondan, bundan kelib chiqadiki, to'g'ri chiziqli koordinatalar tizimini to'liq ortonormal asos orqali aniqlash mumkin. Va bu, ehtimol, haqiqatdir. Formula shunday bo'lishi kerak:

koordinatalar kobi, і ortonormalliklar asosini belgilang Dekart to'g'ri chiziqli tekislik koordinata tizimi . Bu to'g'ri chiziqli koordinatalar tizimi albatta bitta nuqta va ikkita bitta ortogonal vektor bilan ifodalanadi. Siz buni stulning o'zida ko'rasiz, men o'rganganimdek - geometrik ishlarda vektor va koordinata o'qlari ko'pincha (lekin har doim ham emas) chiziladi.

Menimcha, hamma nuqtadan (koordinatalardan) tashqari ortonormal asos borligini tushundi SAVOLNING NOKTASI BO'LING VA SAVOLNING VEKTORI BO'LING koordinatalarini belgilash mumkin. Majoziy ma'noda aytganda, "kvadratdagi hamma narsani raqamlash mumkin".

Koordinata vektorlari bitta bo'lishi kerakmi? Yo'q, ular juda ko'p pul to'lashlari mumkin. Nolga teng bo'lmagan qiymatga ega nuqta va ikkita ortogonal vektorni ko'rib chiqaylik:

Bunday asos deyiladi ortogonal. Vektorli koordinatalar to'plami koordinatalar panjarasini belgilaydi va tekislik yoki vektorning istalgan nuqtasi shu asosda uning koordinatalarini kuzatib boradi. Masalan, yoki ... Aniq nomuvofiqlik koordinata vektorlari ekanligidadir zagalny vipadkuda Turli xil dovjinlar mavjud, ular bittaga bo'lingan. Birliklar kattalashishi bilanoq, birlamchi ortonormal asos paydo bo'ladi.

! Eslatma : ortogonal asosda, shuningdek, affin asoslarda ham pastroq, o'qlar bo'ylab birining maydoni va bo'shlig'i hisobga olinadi. UMOVIMI. Masalan, abscissa o'qi bo'ylab bitta birlikda 4 sm, ordinata o'qi bo'ylab bitta birlikda 2 sm.Bu ma'lumot, agar kerak bo'lsa, "nostandart" koordinatalarni "bizning dastlabki santimetrlarimiz" ga tarjima qilish uchun etarli.

Va yana bir oziq-ovqat, chunki haqiqat allaqachon berilgan - 90 darajaga teng bo'lishi mumkin bo'lgan asosiy vektorlar o'rtasidagi bog'liqlik nima? Yo'q! Aybning ma'nosi, asosiy vektorlarini qanday aniqlash mumkin kamroq kolinear emas. Ko'rinishidan, u 0 dan 180 darajagacha bo'lishi mumkin.

Samolyotning nuqtasi deyiladi koordinatalar kobi, і kolinear bo'lmagan vektorlar, , oʻrnating tekislikning affin koordinata tizimi :

Ba'zan bu koordinatalar tizimi deyiladi qiyshiq tizimi. Nuqta va vektor tasviri stulning dumbasi kabi:

Tasavvur qilganingizdek, affin koordinata tizimi bundan ham kamroq qo'lda, u vektorlarni va kesmalarni ikki baravar oshirish formulalari bilan ishlamaydi, biz darsning boshqa qismida ko'rganmiz. Dummies uchun vektorlar, bilan bog'liq boy mazali formulalar vektorlarni skalyar yaratish. Keyin vektorlarni qo'shish va vektorni raqamga ko'paytirishning quyidagi qoidalari, ushbu munosabatdagi kichik bo'lim uchun formulalar, shuningdek, biz qisqacha ko'rib chiqadigan vazifa turidagi harakatlar mavjud.

Va kontseptsiya shundayki, affin koordinatalar tizimini tavsiflashning eng qulay usuli Dekart to'g'ri chiziqli tizimdir. Shuning uchun, azizim, ko'pincha men o'qishim kerak. ...Bu holda, inson hayotida hamma narsa aniq - bu daryoning o'zi (yoki boshqa, masalan, qutbli) koordinatalar tizimi. Gumanoidlar bunday tizimlardan bahramand bo'lishlari mumkin =)

Keling, amaliy qismga o'tamiz. Ushbu darsda berilgan barcha ma'lumotlar to'g'ri chiziqli koordinatalar tizimida ham, afonik shaklda ham adolatli. Bu erda hech qanday murakkab narsa yo'q, barcha materiallar talaba uchun ochiqdir.

Maydon vektorlarining kolinearligi qanday aniqlanadi?

Oddiy boy. Ikki vektor va tekislikka ega bo'lish uchun Agar ular kollinear bo'lsa, ularning koordinatalari proportsional bo'lishi uchun zarur va etarli. Aslida, aniq munosabatlarning koordinatali tafsilotlari yo'q.

Butun 1

a) Vektorlar kollinear ekanligini tekshiring .
b) Chi bazis vektorlarini o'rnatadi ?

Qaror:
a) Vektorlar uchun nimani anglatishi aniq mutanosiblik koeffitsienti, tenglik teng bo'lishi uchun:

O'rnatilgan qoidaning "moda" versiyasi haqida aniq gapiraylik, bu odatda amalda amalga oshiriladi. G'oya darhol mutanosiblikni to'g'irlash va bu haqiqatmi deb hayron bo'lishdir:

Biz vektorlarning tegishli koordinatalari chiziqlaridan nisbatni qo'shamiz:

Qisqacha:
, shuning uchun tashqi koordinatalar proportsionaldir, shuning uchun

O'rnatishni yig'ish va yig'ish mumkin, shuning uchun bir xil variant:

O'z-o'zini tekshirish uchun siz kolinear vektorlar birma-bir chiziqli ifodalanganlarini tekshirishingiz mumkin. Rashkning o'rni kimniki . Ularning adolatini vektorlar bilan elementar harakatlar orqali osongina tekshirish mumkin:

b) Ikkita maydon vektori kolinear (chiziqli mustaqil) bo’lganligi uchun bazis hosil qiladi. Biz vektorlarning kolinearligini kuzatamiz . Biz tizimni yig'amiz:

Birinchisidan tenglama chiqadi, ikkinchisidan esa raqobat chiqadi, keyin esa, tizim absurd(Hech qanday yechim yo'q). Shunday qilib, vektorlarning haqiqiy koordinatalari proportsional emas.

Visnovok: vektorlar chiziqli mustaqil va asos yaratadi.

Yechimning soddalashtirilgan versiyasi quyidagicha ko'rinadi:

Biz vektorlarning mos keladigan koordinatalaridan nisbatni qo'shamiz :
Shuning uchun bu vektorlar chiziqli mustaqil va asos yaratadi.

Ushbu parametr sharhlovchilar tomonidan rad etilganligiga ishonch hosil qiling, aks holda koordinatalar nolga yetsa, muammo paydo bo'ladi. Eksa quyidagicha: . Yoki shunday: . Yoki shunday: . Proporsiya orqali qanday ishlaymiz? (Rostini aytsam, siz nolga bo'lolmaysiz). Aynan shu sababli men soddalashtirilgan yechimni "foppish" deb atadim.

Mavzu: a), b) tasdiqlash.

Mustaqil ijodkorlik uchun kichik ijodiy misol:

Button 2

Vektor parametrining istalgan qiymati uchun kolinearliklar bo'ladimi?

Eritmada parametr proporsiya orqali topiladi.

U vektorlarning kolinearligini tekshirish uchun algebraning takomillashtirilgan usuliga asoslanadi.Biz bilimlarimizni tizimlashtiramiz va beshinchi nuqtani qo'shamiz:

Maydonning ikkita vektori uchun qattiqlashuvning ekvivalent bosqichlari:

2) vektorlar asosni belgilaydi;
3) vektorlar kolinear emas;

+ 5) birlamchi, nolga bo'ysunuvchi ushbu vektorlarning koordinatalarini qo'shish.

Aftidan, ekvivalent oyoq va yotoq qattiqligi:
1) chiziqli vektorlar;
2) vektorlar bazisga teng emas;
3) vektorlar kolinear;
4) vektorlarni bittadan bittaga chiziqli ifodalash mumkin;
+ 5) birlamchi, bu vektorlarning koordinatalaridan qo'shish, nolga teng.

Ishonchim komilki, siz allaqachon tanish bo'lgan barcha shartlar va bayonotlarni tushungansiz.

Keling, hisobotning yangi, beshinchi bandini ko'rib chiqaylik: maydonning ikkita vektori Kolinear usullar va faqat bu vektorlarning koordinatalaridan nolga nisbatan buklangan bo'lsa,:. Ushbu belgilarni bajarish uchun, albatta, e'tiborga olishingiz kerak bilish va g'alaba qozonish.

Virishimo Butt 1 boshqa yo'l bilan:

a) Vektorlar koordinatalarini qo'shish kovariati hisoblanadi :
, u holda vektorlar kollineardir.

b) Ikkita maydon vektori kolinear (chiziqli mustaqil) bo’lganligi uchun bazis hosil qiladi. Vektor koordinatalarining kovariati hisoblash mumkin :
, Shuningdek, vektorlar chiziqli mustaqil va asos yaratadi.

Mavzu: a), b) tasdiqlash.

U kamroq nisbatlar bilan ancha ixcham va chiroyli ko'rinadi.

Ko'rib chiqilgan material yordamida vektorlarning kolinearligini o'rnatish, kesmalar va to'g'ri chiziqlar parallelligini o'rnatish mumkin. Keling, aniq geometrik raqamlar bilan bir nechta buyurtmalarni ko'rib chiqaylik.

Butun 3

Chotirikutnikning tepalarini hisobga olgan holda. Chotirikutnik parallelogramm ekanligini menga xabar bering.

Tugallandi: Muammoda kresloga ehtiyoj qolmaydi, yechimning qolgan qismi faqat analitik boʻladi Belgilangan parallelogrammni taxmin qilish mumkin:
Paralelogramma U chotirikutnik deb ataladi, uning yon tomonlari juft parallel.

Shu tarzda etkazish kerak:
1) proksimal tomonlarning parallelligi;
2) qarama-qarshi tomonlarning parallelligi.

Ishonchli:

1) Biz vektorlarni bilamiz:

2) Biz vektorlarni bilamiz:

Vishov bir xil vektor ("maktab bo'yicha" - teng vektorlar). Kolinearlik allaqachon aniq, ammo qarorni aniq, yaxshi tartibga solingan tarzda rasmiylashtirish yaxshiroqdir. Vektorlar koordinatalarini qo'shish kovariati hisoblanadi:
, Shuningdek, vektorlar kollinear va .

Visnovok: Qayinning qarama-qarshi tomonlari juft bo'lib parallel, shuning uchun ma'nolar orqasida parallelogramma mavjud. Nimani tarbiyalash kerak edi.

Yana yaxshi va turli raqamlar:

Butun 4

Chotirikutnikning tepalarini hisobga olgan holda. Chotirikutnik trapezoid ekanligini bizga xabar bering.

Dalilni yaxshiroq shakllantirish uchun katta trapezoidni olish kerak yoki shunchaki o'tirib, uning qanday ko'rinishini taxmin qilish kerak.

Bu mustaqil qarorning maqsadi. Eng muhimi, yechim darsga o'xshaydi.

Va endi asta-sekin maydondan ochiq maydonga o'tish vaqti keldi:

Kosmosdagi vektorlarning kolinearligini qanday aniqlash mumkin?

Qoida juda o'xshash. Ikki fazo vektori kolinear boʻlishi uchun ularning nisbiy koordinatalari proportsional boʻlishi zarur va yetarlidir..

Butun 5

Bilingki, kolinear vektorlar kosmosda mavjud bo'ladi:

A);
b)
V)

Qaror:
a) Tegishli vektor koordinatalari uchun proportsionallik koeffitsienti nima ekanligini tekshiramiz:

Tizimda yechim yo'q, chunki vektorlar kolinear emas.

"Sproshchenka" nisbatlarni teskari o'zgartirish orqali rasmiylashtiriladi. Ushbu bo'limda:
- koordinatalar proportsional emas va vektorlar kolinear emas.

Mavzu: vektorlar kolinear emas.

b-c) Bular mustaqil qaror qabul qilish nuqtalari. Uni ikki xil usulda loyihalashga harakat qiling.

Maqolada ko'rsatilgan usulni hisobga olgan holda, kosmik vektorlarni kolinearlik va uchinchi tartib kelib chiqishi orqali tekshirish usuli mavjud. Vektorli tv vektorlar.

Yassi kesimga o'xshab, ko'rib chiqilayotgan asboblarni fazoviy kesmalar va to'g'ri chiziqlar parallelligini kuzatish orqali yig'ish mumkin.

Boshqa bo'limni so'raymiz:

Trivial fazoda vektorlarning lineerligi va mustaqilligi.
Kengaytirilgan bazis va affin koordinatalar tizimi

Biz tekislikda ko'rgan ko'plab naqshlar ochiq maydonda adolatli bo'ladi. Men nazariyadan abstraktni minimallashtirishga harakat qildim, ma'lumotlarning chap qismining qismlari allaqachon aniqlangan. Tim, kam emas, men sizga kirish qismini diqqat bilan o'qib chiqishingizni tavsiya qilaman, chunki yangi atamalar va tushunchalar kiritiladi.

Endi kompyuter stolining maydoni o'rniga uch o'lchamli bo'sh joy mavjud. Keling, bundan buyon shu asosni yarataylik. Biz uyda yoki ko'chada bo'lamizmi, biz hech qachon kenglik, chuqurlik va balandlikning uchta dunyosini uchrata olmaymiz. Shuning uchun, asos yaratish uchun uchta kosmik vektor kerak. Bir yoki ikkita vektor etarli emas, choraklar juda yaxshi.

Yana barmoqlarimga yoğrayman. Mehribon bo'ling, qo'lingizni yuqoriga ko'taring va turli tomonlaringizni oching ajoyib, ta'sirchan va o'rta barmoq. Vektorlar bo'ladi, turli tomondan hidlar paydo bo'ladi, bir-birining o'rtasida turli xil farqlar bo'ladi va bir-biridan turli xil hidlar bo'ladi. Qarasam, arzimas kenglikning asosi tayyor! Gapirishdan oldin, hisob qaydnomangizga bunday narsani ko'rsatishning hojati yo'q, shunchaki barmoqlaringizni aylantirmang va siz hech qayerga erisha olmaysiz =)

Kelajakda muhimroq ovqatni qo'yaylik, trivial makonning asosini yaratadigan uchta vektor bo'lsin? Mehribon bo'ling, kompyuter stolining yon tomoniga uchta barmog'ingizni mahkam bosing. Nima bo'ldi? Uchta vektor bir tekislikda harakat qildi va taxminan aytganda, biz yo'qolgan dunyolardan birini - balandlikni bilardik. Bunday vektorlar o'xshash Va arzimas makonning asosini yaratib bo'lmasligi butunlay ayon.

Shuni ta'kidlash kerakki, koplanar vektorlar bir tekislikda yotmaydi, lekin parallel tekisliklarda joylashgan bo'lishi mumkin (barmoqlaringiz bilan ishlang, shuning uchun Salvador Dali uchun bu qiyinroq =)).

Viznachennya: vektorlar deyiladi o'xshash Sifatida hidga parallel bo'lgan tekislik bor. Bu erda shuni qo'shish mantiqan to'g'riki, agar bunday maydon bo'lmasa, vektorlar koplanar bo'lmaydi.

Uchta koplanar vektor har doim chiziqli bo'ladi keyin ular birma-bir chiziqli ifodalanadi. Oddiylik uchun yana bir bor yomon hidning xuddi shu hududda joylashganligi qabul qilinadi. Avvalo, faqat koplanar bo'lmagan vektorlar ham kolinear bo'lishi mumkin, shuning uchun har qanday vektor har qanday vektor orqali ifodalanishi mumkin. Boshqa holatda, masalan, vektorlar to'g'ri chiziqli emasligi sababli, uchinchi vektor ular orqali bitta shaklda ifodalanadi: (Nima uchun oldingi qismdagi materiallardan taxmin qilish oson).

Bu burilish nuqtasi adolatli: uchta koplanar bo'lmagan vektor har doim chiziqli mustaqildir, ular o'zlarini birma-bir ifoda etmasliklari uchun. Va, shubhasiz, faqat bunday vektorlar ahamiyatsiz bo'shliqning asosini yaratishi mumkin.

Viznachennya: Trivial makonning asosi chiziqli mustaqil (komplanar bo'lmagan) vektorlar uchligi deyiladi, kuylash tartibidan olingan fazo vektori qanday bo'lishidan qat'iy nazar bir martabada berilgan asosda parchalanadi, bu erda vektorning koordinatalari shu asosda

O'ylaymanki, siz ko'rinishdagi vakillik vektorini ham aytishingiz mumkin chiziqli birikma asosiy vektorlar.

Koordinatalar tizimi kontseptsiyasi xuddi tekis chizma bilan bir xil tarzda kiritilgan, bitta nuqta yoki uchta chiziqli mustaqil vektor etarli:

koordinatalar kobi, і tekis bo'lmagan vektorlar, kuylash tartibidan olingan, oʻrnating trivial fazoning affin koordinata tizimi :

Albatta, "o'ralgan" koordinata panjarasi juda qulay emas, lekin koordinatalar tizimi bizga imkon beradi albatta har qanday vektorning koordinatalarini va fazodagi istalgan nuqtaning koordinatalarini bildiradi. Samolyotga o'xshab, affin koordinatalar tizimida bo'shliq men allaqachon o'ylagan ba'zi formulalarni qayta ishlamaydi.

Affin koordinata tizimining eng muhim va to'g'ridan-to'g'ri ta'rifi kosmosga to'g'ri chiziqli koordinatalar tizimi:

Kosmos nuqtasi, deyilganidek koordinatalar kobi, і ortonormalliklar asosini belgilang Dekart to'g'ri chiziqli koordinatalar tizimi . Rasmni bilish:

Amaliy vazifalarga o'tishdan oldin, biz yana ma'lumotlarni tizimlashtiramiz:

Kosmosdagi uchta vektor uchun bir xil qattiq jismlar ekvivalentdir:
1) vektorlar chiziqli mustaqil;
2) vektorlar asosni belgilaydi;
3) vektorlar koplanar emas;
4) vektorlarni bir-biri orqali chiziqli ifodalash mumkin emas;
5) birlamchi, bu vektorlarning koordinatalarini noldan katlama.

To'shakdagi yaralar, menimcha, tozalangan.

Kosmosdagi vektorlarning chiziqli joylashuvi/mustaqilligi an'anaviy ravishda qo'shimcha manba yordamida tekshiriladi (5-band). Yo'qotilgan amaliy bilimlar aniq algebraik xususiyatga ega. Geometrik kalitni gullarga osib qo'yish va chiziqli algebrani beysbol tayoqchasi bilan ishlatish vaqti keldi:

Uch vektorli fazo koplanar usullar va faqat ushbu vektorlarning koordinatalarini qo'shishning kelib chiqishi nolga teng bo'lsa: .

Men kichik bir texnik nuanceni ta'kidlamoqchiman: vektorlarning koordinatalari nafaqat ustunda, balki qatorda ham yozilishi mumkin (birlamchining qiymati o'zgarmaydi - birlamchilarning ajoyib kuchi). Ale qolganlarga qaraganda ancha chiroyli, bu uni ko'plab amaliy vazifalarni bajarish uchun qulayroq qiladi.

Asl nusxalarni saralash usullarini unutgan va ularga yomon yo'naltirilgan bo'lishi mumkin bo'lgan o'quvchilarga men eng qadimgi darslarimdan birini tavsiya qilaman: Qiymatni qanday hisoblaysiz?

Butun 6

Quyidagi vektorlar ahamiyatsiz bo'shliqning asosini yaratishini tekshiring:

Qaror: Aslida, barcha qarorlar asosiy qarzni to'lashdan kelib chiqadi

a) vektorlar koordinatalaridan olingan qo'shimchalarning xulosasi hisoblanishi mumkin (birinchi qatordagi mezonlarning natijasi):

, Shuningdek, vektorlar chiziqli mustaqil (komplanar emas) va trivial fazoning asosini yaratadi.

Vídpovid: ma'lumotlar vektorlari va bazasi

b) Bu mustaqil qarorning nuqtasi. Eng muhimi, darsning yechimi va xulosasi bor.

Tuzoqlar va ijodiy harakatlar:

Button 7

Parametrning qaysi qiymati uchun vektorlar koplanar bo'ladi?

Qaror: Vektorlar koplanar bo'lib, faqat bu vektorlarning koordinatalarining koordinatalarining qo'shilishi nolga teng bo'lsa:

Aslida rahbarga sodiq bo'lish kerak. Biz jerboasdagi fokuslar kabi nolga erishamiz - eng aniq narsa uni boshqa qatorda ochish va darhol kamchiliklar bo'ladi:

Biz keyingi soddalashtirishni amalga oshiramiz va uni o'ngdan eng oddiy chiziqli tenglamaga qisqartiramiz:

Vídpovid: da

Bu erda teskari o'zgartirishni amalga oshirish oson, buning uchun siz chiqish manbasidagi qiymatlarni almashtirishingiz va qayta o'zgartirishingiz kerak. , uni yana ochgan.

Nihoyat, biz yana bir tipik masalani ko'rib chiqamiz, u ko'proq algebraik xususiyatga ega va chiziqli algebra kursidan oldin kiritilishi kerak. Jadvalning yuqori qismi keng bo'lib, u keyingi yuqoriga loyiqdir:

Keling, 3 ta vektor ahamiyatsiz bo'shliqning asosini yaratadi
va shu asosda 4-vektorning koordinatalarini biling

Button 8

Berilgan vektorlar. Vektorlar trivial fazoning asosini tashkil etishini ko'rsating va shu asosda vektorning koordinatalarini toping.

Qaror: Keling, avvalo ongga qaraylik. Aqlning orqasida to'rtta vektor mavjud va siz bilganingizdek, xuddi shu asosda allaqachon koordinatalar mavjud. Bu asos - bizni bezovta qilmang. Va buni shunday ifodalash uchun: uchta vektor bir butun sifatida yangi asos yaratishi mumkin. Birinchi bosqich 6-ilovadagi echimlardan butunlay chetlab o'tilgan, vektorlarning haqiqatan ham chiziqli mustaqilligini tekshirish kerak:

Vektorlar koordinatalarini qo'shish kovariati hisoblanadi:

, Shuningdek, vektorlar chiziqli mustaqil bo'lib, ahamiyatsiz bo'shliqning asosini yaratadi.

! Muhim : vektor koordinatalari obov'yazkovo yozilishi mumkin stantsiyasida birinchisi, qatorlarda emas. Aks holda, ochishning keyingi algoritmida chalkashlik bo'ladi.

Viraz aql chaqirdi vektorlarning chiziqli birikmasi A 1 , A 2 ,..., A n koeffitsientlar bilan l 1, l 2 ,...,l n.

Vektor tizimining chiziqli pozitsiyasining qiymatlari

Vektor tizimi A 1 , A 2 ,..., A n chaqirdi chiziqli ravishda yotqizilgan, Nolga teng bo'lmagan raqamlar to'plami nima? l 1, l 2 ,...,l n, vektorlarning har qanday chiziqli birikmasi uchun l 1 *A 1 +l 2 *A 2 +...+l n *A n nol vektordan kattaroq, Keyin darajalar tizimi: Nolga teng bo'lmagan qaror mavjud.
Raqamlarni tering l 1, l 2 ,...,l n ê nolga teng emas, agar siz raqamlardan birini xohlasangiz l 1, l 2 ,...,l n noldan o'zgartirish.

Vektor tizimining chiziqli mustaqilligi qiymatlari

Vektor tizimi A 1 , A 2 ,..., A n chaqirdi chiziqli mustaqil, bu vektorlarning chiziqli birikmasi sifatida l 1 *A 1 +l 2 *A 2 +...+l n *A n noldan ko'p vektor nol raqamlar to'plamidan ko'proq l 1, l 2 ,...,l n , Keyin darajalar tizimi: A 1 x 1 +A 2 x 2 +...+A n x n =D Faqat bitta yechim bor.

Aksiya 29.1

Bu vektorlarning chiziqli tizimi ekanligini tekshiring

Qaror:

1. Biz darajalar tizimini yaratamiz:

2. Gauss usuli bilan tasdiqlangan. Jordano tizimining transformatsiyasi 29.1-jadvalda ko'rsatilgan. Tizimning o'ng qismi kengaytirilganda, fragmentlar yozilmaydi, ular nolga etadi va Iordaniya o'zgarishlari tufayli o'zgarmaydi.

3. Jadvalning qolgan uchta qatori ruxsat etilgan tizimni qayd qiladi, chiqishga teng tizim:

4. Tizimning yashirin yechimi yo'q qilinadi:

5. Hokimiyatdan erkin o'zgarish qiymatini so'rab, x 3 =1, Nolga teng bo'lmagan qarorlar qat'iyan chiqarib tashlanadi X = (-3,2,1).

Dalil: Shunday qilib, nolga teng bo'lmagan sonlar to'plami (-3,2,1) bilan vektorlarning chiziqli birikmasi nol vektor -3A1+2A2+1A3=T ga teng. Otje, vektorlar tizimi chiziqli bog'liqdir.

Vektor tizimlarining kuchi

Quvvat (1)
Agar vektorlar sistemasi chiziqli bo`ysunuvchi bo`lsa, u holda vektorlardan biri boshqalardan keyin parchalansa, sistema vektorlaridan biri boshqalardan keyin parchalansa, vektorlar sistemasi chiziqli bo`ysunuvchi bo`ladi.

Quvvat (2)
Vektorlarning har bir quyi tizimi chiziqli bog'liq bo'lganligi sababli, butun tizim chiziqli bog'liqdir.

Quvvat (3)
Agar vektorlar tizimi chiziqli mustaqil bo'lsa, quyi tizim chiziqli mustaqildir.

Hokimiyat (4)
Nol vektorni o'z ichiga olgan vektorlar tizimi mavjudmi, u chiziqli eskirgan.

Hokimiyat (5)
m o'lchamli vektorlar tizimi har doim chiziqli bo'ladi, agar n vektorlar soni ularning o'lchamidan (n>m) katta bo'lsa.

Vektor tizimining asoslari

Vektor tizimining asosi A 1 , A 2 ,..., A n bunday quyi tizim B 1 , B 2 ,..., B r deyiladi.(B 1, B 2,..., B r vektorlaridan biri A 1, A 2,..., A n vektorlaridan biri), bu kunning ongini qondiradi:
1. B 1 ,B 2 ,...,B r vektorlarning chiziqli mustaqil tizimi;
2. nima bo'lishidan qat'iy nazar vektor A j A 1 , A 2 ,..., A n sistemalar B 1 , B 2 ,..., B r vektorlari orqali chiziqli ifodalanadi.

r- bazaga kiritilgan vektorlar soni.

Teorema 29.1 Vektorlar sistemasining unitar asosi haqida.

Agar m o‘lchamli vektorlar sistemasida m xil E 1 E 2,..., E m bitta vektor bo‘lsa, ularning barchasi sistemaning asosini yaratadi.

Vektor sistemasining asosini topish algoritmi

A 1 , A 2 ,..., A n vektor sistemasining asosini bilish uchun quyidagilar zarur:

• Yagona vektorlar tizimini yagona darajalar tizimiga katlayın A 1 x 1 +A 2 x 2 +...+A n x n =D
• Qiu tizimini tanishtiring

Vektorlarning chiziqli birikmasi vektor deyiladi
, de 1, ... , m - etarli koeffitsientlar.

Vektor tizimi
asosiy chiziqli birikma teng bo'lgani uchun chiziqli eskirgan deb ataladi Bunday holda biz bitta nolga teng bo'lmagan koeffitsientni xohlaymiz.

Vektor tizimi
chiziqli mustaqil deb ataladi, chunki har qanday chiziqli birikmada qadimgi barcha koeffitsientlar nolga teng.

Vektor tizimining asosi
Bu tizim vektori sifatida belgilanishi mumkin bo'lgan bo'sh bo'lmagan chiziqli mustaqil quyi tizim deb ataladi.

2-misol. Vektor sistemasining asosini toping = (1, 2, 2, 4),= (2, 3, 5, 1),= (3, 4, 8, -2),= (2, 5, 0, 3) va boshqa vektorlarni bazis orqali ifodalang.

Rozv'yazannya. Keling, ushbu vektorlarning koordinatalarini ustunlar bilan kengaytirish mumkin bo'lgan matritsa yarataylik. Keling, buni bosqichma-bosqich ko'rib chiqaylik.

~
~
~
.

Ushbu tizimning asosini vektorlar belgilaydi ,,, Aylanalarda ko'rsatilgan qatorlarning Supero'tkazuvchilar elementlari bilan ifodalanadi. Vektor aylanish uchun X 1 ga teng bo'lishi mumkin +x 2 + x 4 =. U chiziqli darajalar tizimiga tushiriladi, uning matritsasi ustunning chiqish almashinuvidan kelib chiqadi, bu ko'rsatadi joyda erkin a'zolar yig'ilishi bor. Shuning uchun tizimni yakunlash uchun matritsa bosqichma-bosqich ko'rinishdan olingan, unda kerakli almashtirishlar amalga oshirilgan.

Doimiy ma'lum:

x1+4=3, x1=-1;

= -+2.

Eslatma 1. Agar bir qancha vektorlar asosi orqali ifodalash zarur bo'lsa, u holda ularning har biri uchun o'xshash chiziqli darajalar tizimi bo'ladi. Ushbu tizim faqat uning a'zolarining ko'pchiligi tomonidan demontaj qilinadi. Shuning uchun, ularni maksimal darajada oshirish uchun siz bir nechta turli a'zolarni o'z ichiga olgan bitta matritsani katlashingiz mumkin. Kimning teri tizimi boshqalardan farq qiladi.

Hurmat 2. Har qanday vektorni o'zgartirish uchun uning oldida turgan tizimning bazis vektorlarini vikorizatsiya qilish kifoya. Bunday holda, matritsani qayta shakllantirishning hojati yo'q, kerakli joyga vertikal chegara qo'yish kifoya.

2. Vektor sistemasining asosini toping va bazis orqali boshqa vektorlarni ifodalang:

A) = (1, 3, 2, 0),= (3, 4, 2, 1),= (1, -2, -2, 1),= (3, 5, 1, 2);

b) = (2, 1, 2, 3),= (1, 2, 2, 3),= (3, -1, 2, 2),= (4, -2, 2, 2);

V) = (1, 2, 3),= (2, 4, 3),= (3, 6, 6),= (4, -2, 1);= (2, -6, -2).

1. 3. Yechimlarning fundamental tizimi

Chiziqli tenglamalar sistemasi bir jinsli deyiladi, chunki uning erkin hadlari nolga teng.

Chiziqli sathlarning bir qatorli tizimini ajratishning asosiy tizimi uzilishlarning shaxssizligining asosi deb ataladi.

Keling, sizga chiziqli darajalarning geterogen tizimini beraylik. Qiymat bilan bog'langan yagona tizim barcha nol a'zolarni nolga almashtirish orqali yo'q qilinadigan tizimdir.

Geterogen sistema kogerent va ahamiyatsiz bo'lgani uchun uning ko'proq qoniqarli yechimi f n +  1 f o1 + ... +  k f o k kabi ko'rinadi, def n – geterogen tizimning xususiy yechimi i f o1 , ... , f o k asosiy hisoblanadi. bog'langan yagona tizimning tizimli yechimi

O'RNAK 3. 1-misoldagi geterogen sistemaning yechimi va bog'langan bir jinsli sistemaning asosiy sistemasi haqida bilib oling.

Qaror. Biz 1-ilovada olingan yechimni vektor ko'rinishida yozamiz va yangidagi qo'shimcha parametrlarni va belgilangan raqamli qiymatlarni jamlab, eng yuqori vektorni kengaytiramiz:

= (x 1 , x 2 , x 3 , x 4) = (–2a + 7b – 2, a, –2b + 1, b) = (–2a, a, 0, 0) + (7b, 0, – 2b, b) + + (-2, 0, 1, 0) = a (-2, 1, 0, 0) + b (7, 0, -2, 1) + (- 2, 0, 1, 0) ).

f n = (-2, 0, 1, 0), f o1 = (-2, 1, 0, 0), f o2 = (7, 0, -2, 1) ni yo'q qiling.

Hurmat. Xuddi shunday, bir jinsli tizimni yechish uchun fundamental tizimni topish muammosi kutilmoqda.

3.1 Bir jinsli sistemaning asosiy tizimini va yechimini bilish:

A)

b)

c) 2x1 – x2+3x3=0.

MASHQ 3.2. Geterogen sistemaning xususiy yechimini va bogʻlangan bir jinsli sistema yechimining asosiy tizimini toping:

A)

b)

Bazisga kirmagan vektorlar va vektorlar sistemasining asosini toping, bazis bo'yicha tartiblang:

A 1 = {5, 2, -3, 1}, A 2 = {4, 1, -2, 3}, A 3 = {1, 1, -1, -2}, A 4 = {3, 4, -1, 2}, A 5 = {13, 8, -7, 4}.

Qaror. Keling, chiziqli darajalarning yagona tizimini ko'rib chiqaylik

A 1 X 1 + A 2 X 2 + A 3 X 3 + A 4 X 4 + A 5 X 5 = 0

yoki qizg'in ko'rinish .

Biz ushbu tizimni Gauss usuli bilan, qatorlar va ustunlarni almashtirmasdan tekshiramiz va qo'shimcha ravishda, bosh elementni yuqori chap burchakda emas, balki butun qatorda tanlaymiz. Cho'l shundan iborat aylantirilgan vektor tizimining diagonal qismiga qarang.

~ ~

~ ~ ~ .

Vektorlar tizimiga ruxsat berilgan, u chiqishga teng, o'xshaydi

A 1 1 X 1 + A 2 1 X 2 + A 3 1 X 3 + A 4 1 X 4 + A 5 1 X 5 = 0 ,

de A 1 1 = , A 2 1 = , A 3 1 = , A 4 1 = , A 5 1 = . (1)

Vektorlar A 1 1 , A 3 1 , A 4 1 diagonal tizimni o'rnating. Ozhe, vektorlar A 1 , A 3 , A 4 vektor tizimining asosini o'rnating A 1 , A 2 , A 3 , A 4 , A 5 .

Endi ochiladigan vektorlar A 2 і A 5 taglik orqasida A 1 , A 3 , A 4 . Buning uchun quyidagi vektorlar yotqizilgan A 2 1 і A Diagonal tizimning orqasida 5 1 A 1 1 , A 3 1 , A 4 1 shuni yodda tutgan holda vektorning parchalanish koeffitsientlari uning koordinatasining diagonal tizimi bo'ylab x i.

Z (1) ma'mo:

A 2 1 = A 3 1 · (-1) + A 4 1 0 + A 1 1 ·1 => A 2 1 = A 1 1 – A 3 1 .

A 5 1 = A 3 1 0 + A 4 1 1 + A 1 1 ·2 => A 5 1 = 2A 1 1 + A 4 1 .

Vektorlar A 2 і A Poydevorning orqasida 5 katlang A 1 , A 3 , A 4 bir xil koeffitsientlar bilan, qaysi vektorlar A 2 1 і A Diagonal tizimning orqasida 5 1 A 1 1 , A 3 1 , A 4 1 (bu koeffitsientlar x i). Otje,

A 2 = A 1 – A 3 , A 5 = 2A 1 + A 4 .

Zavdannya. 1.Bazisga kirmagan vektorlar va vektorlar sistemasining asosini toping, bazis bo‘yicha tartiblang:

1. a 1 = { 1, 2, 1 }, a 2 = { 2, 1, 3 }, a 3 = { 1, 5, 0 }, a 4 = { 2, -2, 4 }.

2. a 1 = { 1, 1, 2 }, a 2 = { 0, 1, 2 }, a 3 = { 2, 1, -4 }, a 4 = { 1, 1, 0 }.

3. a 1 = { 1, -2, 3 }, a 2 = { 0, 1, -1 }, a 3 = { 1, 3, 0 }, a 4 = { 0, -7, 3 }, a 5 = { 1, 1, 1 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

2. Vektor tizimining barcha asoslarini toping:

1. a 1 = { 1, 1, 2 }, a 2 = { 3, 1, 2 }, a 3 = { 1, 2, 1 }, a 4 = { 2, 1, 2 }.

2. a 1 = { 1, 1, 1 }, a 2 = { -3, -5, 5 }, a 3 = { 3, 4, -1 }, a 4 = { 1, -1, 4 }.