Векторний витвір- це псевдовектор, перпендикулярний до площини, побудованої по двох співмножниках, що є результатом бінарної операції «векторне множення» над векторами в тривимірному Евклідовому просторі. Векторний твір не має властивості комутативності та асоціативності (є антикомутативним) і, на відміну від скалярного твору векторів, є вектором. Широко використовується в багатьох технічних та фізичних додатках. Наприклад, момент імпульсу і сила Лоренца математично записуються як векторного твори. Векторний добуток корисний для «вимірювання» перпендикулярності векторів - модуль векторного добутку двох векторів дорівнює добутку їх модулів, якщо вони перпендикулярні, і зменшується до нуля, якщо вектори паралельні або антипаралельні.
Визначити векторний добуток можна по-різному, і теоретично, у просторі будь-якої розмірності n можна обчислити добуток n-1 векторів, отримавши при цьому єдиний вектор, перпендикулярний до них усім. Але якщо твір обмежити нетривіальними бінарними творами з векторними результатами, то традиційний векторний твір визначено лише у тривимірному та семимірному просторах. Результат векторного твору, як і скалярного, залежить від метрики Евклідова простору.
На відміну від формули для обчислення за координатами векторів скалярного добутку у тривимірній прямокутній системі координат, формула для векторного добутку залежить від орієнтації прямокутної системи координат або, інакше, її «хіральності».
Визначення:
Векторним добутком вектора a вектор b у просторі R 3 називається вектор c , що задовольняє наступним вимогам:
довжина вектора c дорівнює добутку довжин векторів a і b на синус кута між ними:
|c|=|a||b|sin φ;
вектор c ортогональний кожному з векторів a і b;
вектор c спрямований так, що трійка векторів abc є правою;
у разі простору R7 потрібна асоціативність трійки векторів a, b, c.
Позначення:
c===a × b

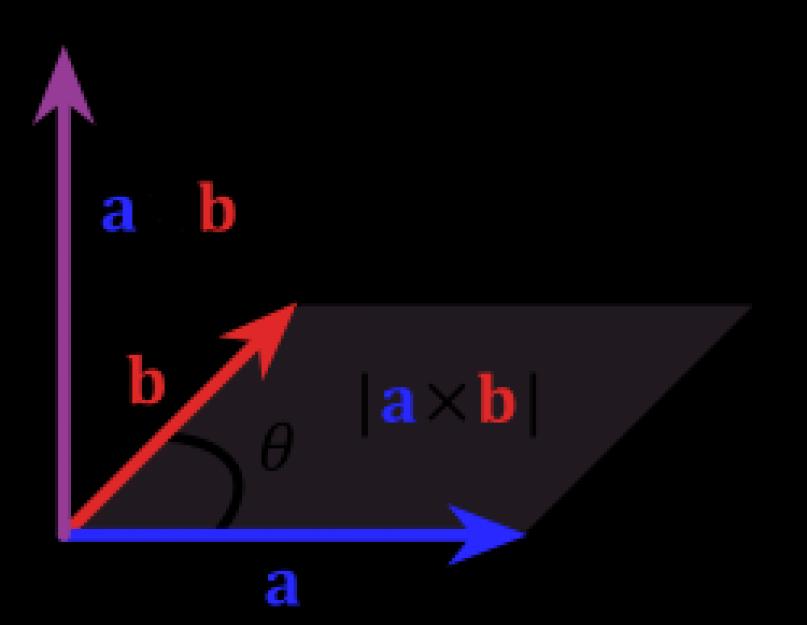
Мал. 1. Площа паралелограма дорівнює модулю векторного твору
Геометричні властивості векторного твору:
Необхідною та достатньою умовою колінеарності двох ненульових векторів є рівність нуля їхнього векторного твору.
Модуль векторного твору дорівнює площі Sпаралелограма, побудованого на приведених до загального початку векторах aі b(Див. рис.1).
Якщо e- одиничний вектор, ортогональний вектор aі bі вибраний так, що трійка a,b,e- права, а S- площа паралелограма, побудованого на них (наведених до загального початку), то для векторного твору справедлива формула:
=S e
Рис.2. Об'єм паралелепіпеда при використанні векторного та скалярного добутку векторів; пунктирні лінії показують проекції вектора c на a × b та вектора a на b × c, першим кроком є знаходження скалярних творів
Якщо c- якийсь вектор, π
- будь-яка площина, що містить цей вектор, e- одиничний вектор, що лежить у площині π
та ортогональний до c,g- одиничний вектор, ортогональний до площини π
і спрямований так, що трійка векторів ecgє правою, то для будь-кого, хто лежить у площині π
вектора aсправедлива формула:
=Pr e a |c|g
де Pr e a векторна проекція e на a
|c|-модуль вектора з
При використанні векторного та скалярного творів можна вирахувати обсяг паралелепіпеда, побудованого на приведених до загального початку векторах a, bі c. Такий добуток трьох векторів називається змішаним.
V=|a (b×c)|
На малюнку показано, що цей обсяг може бути знайдений двома способами: геометричний результат зберігається навіть при заміні «скалярного» та «векторного» творів місцями:
V=a×b c=a b×c
Величина векторного твору залежить від синуса кута між початковими векторами, тому векторний твір може сприйматися як ступінь перпендикулярності векторів так само, як і скалярний твір може розглядатися як ступінь паралельності. Векторний добуток двох одиничних векторів дорівнює 1 (поодинокому вектору), якщо початкові вектори перпендикулярні, і дорівнює 0 (нульовому вектору), якщо вектори паралельні або антипаралельні.
Вираз для векторного твору в декартових координатах
Якщо два вектори aі bвизначені своїми прямокутними декартовими координатами, а точніше - представлені в ортонормованому базисі
a = (a x, a y, a z)
b = (b x, b y, b z)
а система координат права, то їхній векторний твір має вигляд
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Для запам'ятовування цієї формули:
i = ∑ε ijk a j b k
де ε ijk- символ Леві-Чівіти.
Визначення. Векторним твором вектора а (множинне) на колінеарний йому вектор (множник) називається третій вектор з (твір), який будується наступним чином:
1) його модуль чисельно дорівнює площі паралелограма на рис. 155), побудованого на векторах тобто він дорівнює напрям перпендикулярно площині згаданого паралелограма;
3) при цьому напрям вектора з вибирається (з двох можливих) так, щоб вектори складали праву систему (§ 110).
Позначення: або
Доповнення до визначення. Якщо вектори колінеарні, то фігурі вважаючи її (умовно) паралелограмом, звичайно приписати нульову площу. Тому векторний добуток колінеарних векторів вважається рівним нуль-вектору.

Оскільки нуль-вектору можна приписати будь-який напрямок, ця угода не суперечить пунктам 2 та 3 визначення.
Зауваження 1. У терміні «векторний твір» перше слово вказує на те, що результат дії є вектором (на противагу скалярному твору; порівн. § 104, зауваження 1).
Приклад 1. Знайти векторний твір, де основні вектори правої системи координат (рис. 156).
1. Оскільки довжини основних векторів дорівнюють одиниці масштабу, то площа паралелограма (квадрату) чисельно дорівнює одиниці. Отже, модуль векторного добутку дорівнює одиниці.
2. Так як перпендикуляр до площини є ось той шуканий векторний твір є вектор, колінеарний вектор; бо обидва вони мають модуль 1, то шуканий векторний добуток дорівнює або k, або -k.
3. З цих двох можливих векторів треба вибрати перший, тому що вектори утворюють праву систему (а вектори ліву).
Приклад 2. Знайти векторний твір
Рішення. Як приклад 1, укладаємо, що вектор дорівнює або k, або -k. Але тепер треба вибрати -k, тому що вектори утворюють праву систему (а вектори ліву). Отже,
Приклад 3. Вектори мають довжини відповідно рівні 80 і 50 см, і утворюють кут 30°. Взявши за одиницю довжини метр, знайти довжину векторного твору

Рішення. Площа паралелограма, побудованого на векторах, дорівнює Довжина шуканого векторного твору дорівнює
Приклад 4. Знайти довжину векторного твору тих самих векторів, взявши за одиницю довжини сантиметр.
Рішення. Оскільки площа паралелограма, побудованого векторах дорівнює то довжина векторного добутку дорівнює 2000 див, тобто.
З порівняння прикладів 3 і 4 видно, що довжина вектора залежить як від довжин сомножителей але й від вибору одиниці довжини.
Фізичний зміст векторного твору.З численних фізичних величин, що зображуються векторним твором, розглянемо лише момент сили.
Нехай А є точка докладання сили Моментом сили щодо точки О називається векторний твір Оскільки модуль цього векторного твору чисельно дорівнює площі паралелограма (рис. 157), то модуль моменту дорівнює добутку основи на висоту, тобто силі, помноженій на відстань від точки О до прямої, вздовж якої діє сила.
У механіці доводиться, що з рівноваги твердого тіла необхідно, щоб дорівнювала нулю як сума векторів , які мають сили, прикладені до тіла, але й сума моментів сил. У тому випадку, коли всі сили паралельні одній площині, складання векторів, що представляють моменти, можна замінити додаванням і відніманням їх модулів. Але за довільних напрямів сил така заміна неможлива. Відповідно до цього векторний добуток визначається саме як вектор, а не як число.


Властивості скалярного твору
Скалярне твір векторів, визначення, властивості
Лінійні операції над векторами.
Вектори, основні поняття, визначення, лінійні операції над ними
Вектором на площині називається впорядкована пара її точок, при цьому перша точка називається початком, а друга кінцем – вектора
Два вектори називаються рівними, якщо вони рівні і сонаправлены.
Вектори, що лежать на одній прямій, називаються сонаправленными якщо вони сонаправленны з одним і тим самим вектором, що не лежать на цій прямій.
Вектори, що лежать на одній прямій або на паралельних прямих, називаються колінеарними, а колінеарні, але не сонаправленные – протилежно-спрямовані.
Вектори, що лежать на перпендикулярних до прямих, називаються ортогональними.
Визначення 5.4. сумою a + b векторів a і b називається вектор, що йде з початку вектора а в кінець вектора b , якщо початок вектора b збігається з кінцем вектора а .
Визначення 5.5. Різниця а - b векторів а і b називається такий вектор з , який у сумі з вектором b дає вектор а .
Визначення 5.6. Творомk a вектора а на число kназивається вектор b , колінеарний вектор а , що має модуль, що дорівнює | k||a |, та напрямок, що збігається з напрямком | а при k>0 і протилежне а при k<0.
Властивості множення вектора на число:
Властивість 1. k(a + b ) = k a+ k b.
Властивість 2. (k + m)a = k a+ m a.
Властивість 3. k(m a) = (km)a .
Слідство. Якщо ненульові вектори а і b колінеарні, то існує таке число k, що b = k a.
Скалярним твором двох ненульових векторів aі bназивається число (скаляр), що дорівнює добутку довжин цих векторів на косинус кута φ між ними. Скалярний твір можна позначати різними способами, наприклад, як ab, a · b, (a , b), (a · b). Таким чином, скалярний добуток дорівнює:
a · b = |a| · | b| · cos φ
Якщо хоча б один із векторів дорівнює нулю, то скалярний добуток дорівнює нулю.
· Властивість перестановки: a · b = b · a(Від перестановки множників скалярне твір не змінюється);
· Властивість розподілу: a · ( b · c) = (a · b) · c(Результат не залежить від порядку множення);
· Властивість поєднання (стосовно скалярного множника): (λ a) · b = λ ( a · b).
· Властивість ортогональності (перпендикулярності): якщо вектора aі bненульові, їх скалярний добуток дорівнює нулю, тільки коли ці вектори ортогональні (перпендикулярні один до одного) a ┴ b;
· Властивість квадрата: a · a = a 2 = |a| 2 (скалярне твори вектора самого із собою дорівнює квадрату його модуля);
· Якщо координати векторів a=(x 1 , y 1 , z 1 ) b=(x 2 , y 2 , z 2 ), то скалярний добуток дорівнює a · b= x 1 x 2 + y 1 y 2 + z 1 z 2.
Вектор проведення векторів. Визначення: Під векторним твором двох векторів і розуміється вектор, для якого:
Модуль дорівнює площі паралелограма, побудованого даних векторах, тобто. , де кут між векторами та
Цей вектор перпендикулярний векторам, що перемножуються, тобто.
Якщо вектори неколлінеарні, вони утворюють праву трійку векторів.
Властивості векторного твору:
1.При зміні порядку співмножників векторний твір змінює свій знак зворотний, зберігаючи модуль, тобто.
2 .Векторний квадрат дорівнює нуль-вектору, тобто.
3 .Скалярний множник можна виносити за символ векторного твори, тобто.
4 .Для будь-яких трьох векторів справедлива рівність
5 .Необхідна і достатня умова колінеарності двох векторів і:
Визначення. Векторним добутком вектора а на вектор b називається вектор, що позначається символом [«, Ь] (або л х Ь), такий, що 1) довжина вектора [а, b] дорівнює (р, де у - кут між векторами а і b ( 2) вектор [а, Ь) перпендикулярний векторам а і Ь, тобто. перпендикулярний площині цих векторів; 3) вектор [а, Ь] спрямований так, що з кінця цього вектора найкоротший поворот від а до b видно тим, що відбувається проти годинникової стрілки (рис. 32). Мал. 32 Рис.31 Інакше кажучи, вектори a, b і [а,Ь) утворюють праву трійку векторів, тобто. розташовані так, як великий, вказівний та середній пальці правої руки. У випадку, якщо вектори а і b колінеарні, вважатимемо, що [а, Ь] = 0. За визначенням довжина векторного твору чисельно дорівнює площі Sa паралелограма (рис. 33), побудованого на векторах, що перемножуються, а і b як на сторонах: 6.1 . Властивості векторного твору 1. Векторний добуток дорівнює нульовому вектору тоді і тільки тоді, коли принаймні один з векторів, що перемножуються, є нульовим або коли ці вектори колінеарні (якщо вектори а і b колінеарні, то кут між ними дорівнює або 0, або 7г). Це легко отримати з того, що Якщо вважати нульовим вектором колінсарним будь-якому вектору, то умова колінеарності векторів а і b можна виразити так 2. Векторний твір антикоммутативно, тобто завжди. Справді, вектори (а, Ь) мають однакову довжину і коллінеарні. Напрямки цих векторів протилежні, оскільки з кінця вектора [а, Ь] найкоротший поворот від а до b буде видно тим, що відбувається проти годинникової стрілки, а з кінця вектора [Ь, а] - за годинниковою стрілкою (рис. 34). 3. Векторний твір має розподільну властивість по відношенню до додавання 4. Числовий множник Л можна виносити за знак векторного твору 6.2. Векторний добуток векторів, заданих координатами Нехай вектори а та Ь задані своїми координатами в базисі. Користуючись розподільчою властивістю векторного твору, знаходимо векторний добуток заданих координатами. Змішаний твір. Випишемо векторні твори координатних ортів (рис. 35): Тому для векторного твору векторів а і b отримуємо з формули (3) наступний вираз Формулу (4) можна записати в символічній формі, що легко запам'ятовується, якщо скористатися визначником 3-го порядку: Розкладаючи цей визначник за елементами 1-го рядка, отримаємо (4). приклади. 1. Знайти площу паралелограма, побудованого на векторах Шукана площа Тому знаходимо = звідки 2. Знайти площу трикутника (рис. 36). Зрозуміло, що площа б"д трикутника ВАТ дорівнює половині площі S паралелограма О АС В. Обчислюючи векторний твір (а, Ь| векторів а = OA і b = оЪ, отримуємо Звідси Зауваження. Векторний твір не асоціативно, тобто рівність ( (а, Ь),с) = [а, |Ь,с)) неправильно, наприклад, при а = ss j маємо § 7. Змішаний добуток векторів Нехай маємо три вектори а, Ь і с. і 1> скторно.В результаті отримаємо вектор [а, 1>].Помножимо його скалярно на вектор з: (к Ь), с) Число ([а, Ь], е) називається змішаним твором векторів а, Ь. і позначається символом (а, 1), е) 7.1 Геометричний зміст змішаного твору Відкладемо вектори а, b і з точки О (рис. 37) Якщо всі чотири точки О, А, В, С лежать в одній площині ( вектори a, b і с називаються в цьому випадку компланарними), то змішане твір ([а, Ь], с) = 0. Це випливає з того, що вектор [а, Ь|перпендикулярний площині, в якій лежать вектори а і 1 », а значить, і вектору с./ Якщо ж т окуляри О, А, В, С не лежать в одній плоскості (вектори a, b і з некомпланарні), побудуємо на ребрах OA, OB та ОС паралелепіпед (рис. 38 а). За визначенням векторного твору маємо (a,b) = So, де So - площа паралелограма OADB, а з - одиничний вектор, перпендикулярний векторам а і Ь і такий, що трійка а, Ь, с - права, тобто. вектори a, b і з розташовані відповідно як великий, вказівний та середній пальці правої руки (рис. 38 б). Помножуючи обидві частини останньої рівності справа скалярно на вектор, отримуємо, що векторний добуток векторів заданих координатами. Змішаний твір. Число ргс дорівнює висоті h побудованого паралелепіпеда, взятого зі знаком «+», якщо кут між векторами с і з гострий (трійка а, Ь, с - права), і зі знаком «-», якщо кут - тупий (трійка а, Ь, с - ліва), так що Тим самим змішаний добуток векторів а, Ь і з дорівнює об'єму V паралелепіпеда, побудованого на цих векторах як на ребрах, якщо трійка а, Ъ, с - права, і -V, якщо трійка а , Ь, з - ліва. Виходячи з геометричного сенсу змішаного твору, можна зробити висновок, що, перемножуючи тс ж вектори a, b і з будь-якому іншому порядку, ми завжди будемо отримувати або +7, або -К. Знак произ- Рис. 38 ведення залежатиме лише від того, яку трійку утворюють вектори, що перемножуються, - праву або ліву. Якщо вектори а, Ь, утворюють праву трійку, то правими будуть також трійки Ь, с, а і с, а, Ь. У той самий час всі три трійки Ь, а, з; а, с, Ь і с, Ь, а – ліві. Тим самим, (а,Ь, с) = (Ь,с, а) = (с,а,Ь) = -(Ь,а,с) = -(а,с,Ь) = -(с,Ь а). Ще раз підкреслимо, що змішаний добуток векторів дорівнює нулю тоді тільки тоді, коли перемножуються вектори а, Ь, з компланарні: (а, Ь, з компланарні) 7.2. Змішаний добуток у координатах Нехай вектори а, Ь, із заданими своїми координатами в базисі i, j, k: а = (x, y, z]), b = (x2, y2> z2), c = (х3, уз,23). Знайдемо вираз для їхнього змішаного твору (а, Ь, с). Маємо змішаний добуток векторів, заданих своїми координатами в базисі i, J, до, дорівнює визначнику третього порядку, рядки якого складені відповідно з координат першого, другого та третього з векторів, що перемножуються. Необхідна і достатня умова компланарності векторів а у \, Z |), b = (х У2. 22), з = (жз, уз, 23) запишеться в наступному вигляді У | z, аг2 у2 -2 = 0. Приклад. Перевірити, чи є компланарними вектори „ = (7,4,6), Ь = (2, 1,1), с = (19, II, 17). Вектори, що розглядаються, будуть компланарні або некомпланарні в залежності від того, дорівнюватиме нулю чи ні визначник Розкладаючи його за елементами першого рядка, отримаємо Д = 7- 6- 4- 15 + 6-3 = 0^- вектори n, Ь, з компланарними. 7.3. Подвійний векторний твір Подвійний векторний твір [а, [Ь, с]] є вектором, перпендикулярним до векторів а і [Ь, с]. Тому він лежить у площині векторів b і с і може бути розкладений цим векторам. Можна показати, що справедлива формула [а, [!>, с]] = Ь(а, е) - с(а, Ь). Вправи 1. Три вектори АВ = с, Ж? = про СА = b служать сторонами трикутника. Виразити через a, b і вектори, що збігаються з медіанами AM, DN, CP трикутника. 2. Якою умовою мають бути пов'язані вектори р і q, щоб вектор р + q ділив кут між ними навпіл? Передбачається, що всі три вектори віднесені до загального початку. 3. Обчисліть довжину діагоналей паралелограма, побудованого на векторах а = 5р + 2q та b = р - 3q, якщо відомо, що | р | = 2v/2, | q | = 3 H-(p7ci) = f. 4. Позначивши через а та b сторони ромба, що виходять із загальної вершини, доведіть, що діагоналі ромба взаємно перпендикулярні. 5. Обчисліть скалярний добуток векторів а = 4i + 7j + 3k та b = 31 - 5j + k. 6. Знайдіть одиничний вектор а0, паралельний вектору а = (6, 7, -6). 7. Знайдіть проекцію вектора a = l + j-kHa вектор b = 21 - j - 3k. 8. Знайдіть косинус кута між векторами IS «ж, якщо А(-4,0,4), В(-1,6,7), С(1,10.9). 9. Знайдіть одиничний вектор р°, одночасно перпендикулярний вектору а = (3, 6, 8) та осі Ох. 10. Обчисліть синус кута між діагоналями паралелофама, побудованого на векторах a = 2i+J-k, b=i-3j + k як на сторонах. Обчисліть висоту h паралелепіпеда, побудованого на векторах а = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k, якщо за основу взято паралелограм, побудований на векторах а та I). Відповіді
ЗМІШАНИЙ ТВОР ТРИХ ВЕКТОРІВ ТА ЙОГО ВЛАСТИВОСТІ
Змішаним творомтрьох векторів називають число, що дорівнює . Позначається ![]() . Тут перші два вектори множаться векторно і потім отриманий вектор скалярно множиться на третій вектор . Очевидно, такий твір є кілька.
. Тут перші два вектори множаться векторно і потім отриманий вектор скалярно множиться на третій вектор . Очевидно, такий твір є кілька.
Розглянемо властивості змішаного твору.
- Геометричний змістзмішаного твору. Змішане твір 3-х векторів з точністю до знака дорівнює обсягу паралелепіпеда, побудованого цих векторах, як у ребрах, тобто. .
Таким чином, і
 .
.
Доведення. Відкладемо вектори від загального початку та побудуємо на них паралелепіпед. Позначимо і зауважимо, що . За визначенням скалярного твору
Припускаючи, що і позначивши через hвисоту паралелепіпеда, знаходимо .
Таким чином, при

Якщо ж, то й. Отже, .
Об'єднуючи обидва ці випадки, отримуємо або .
З підтвердження цієї якості зокрема випливає, що й трійка векторів права, то змішане твір , і якщо – ліва, то .
- Для будь-яких векторів , , справедлива рівність
Доказ цієї властивості випливає із властивості 1. Справді, легко показати, що і . До того ж знаки "+" і "-" беруться одночасно, т.к. кути між векторами та і одночасно гострі або тупі.
- При перестановці будь-яких двох співмножників змішаний твір змінює знак.
Справді, якщо розглянемо змішаний твір, то, наприклад, або
- Змішаний твір тоді і лише тоді, коли один із співмножників дорівнює нулю або вектори – компланарні.
Доведення.
Т.ч., необхідною та достатньою умовою компланарності 3-х векторів є рівність нулю їх змішаного твору. Крім того, звідси випливає, що три вектори утворюють базис у просторі, якщо .
Якщо вектори задані в координатній формі , то можна показати, що їхнє змішане твір знаходиться за формулою:
 .
.Т. о., змішаний добуток дорівнює визначнику третього порядку, у якого в першому рядку стоять координати першого вектора, у другому рядку - координати другого вектора і в третьому рядку - третього вектора.
приклади.
АНАЛІТИЧНА ГЕОМЕТРІЯ У ПРОСТОРІ
Рівняння F(x, y, z)= 0 визначає у просторі Oxyzдеяку поверхню, тобто. геометричне місце точок, координати яких x, y, zзадовольняють цього рівняння. Це рівняння називається рівнянням поверхні, а x, y, z- поточними координатами.
Однак, часто поверхня задається не рівнянням, а як безліч точок простору, що мають ту чи іншу властивість. І тут потрібно знайти рівняння поверхні, з її геометричних властивостей.
ПЛОЩІСТЬ.
НОРМАЛЬНИЙ ВЕКТОР ПЛОЩИНИ.
РІВНЯННЯ ПЛОЩИНИ, ЩО ПРОХОДИТЬ ЧЕРЕЗ ДАНУ ТОЧКУ
Розглянемо у просторі довільну площинуσ. Її положення визначається завданням вектора , перпендикулярного цій площині, та деякої фіксованої точки M 0(x 0, y 0, z 0), що лежить у площині σ.

Вектор перпендикулярний площині σ називається нормальнимвектор цієї площини. Нехай вектор має координати.
Виведемо рівняння площини σ, що проходить через цю точку M 0і має нормальний вектор. Для цього візьмемо на площині σ довільну точку M(x, y, z)і розглянемо вектор.
Для будь-якої точки MÎ σ вектор .Тому їх скалярний добуток дорівнює нулю. Ця рівність – умова того, що точка MÎ σ. Воно справедливе для всіх точок цієї площини і порушується, як тільки точка Mопиниться поза площиною σ.
Якщо позначити через радіус-вектор точки M, – радіус-вектор точки M 0, то й рівняння можна записати у вигляді
Це рівняння називається векторнимрівнянням площини. Запишемо його у координатній формі. Оскільки , то
Отже, ми отримали рівняння площини, що проходить цю точку. Таким чином, для того, щоб скласти рівняння площини, потрібно знати координати нормального вектора та координати деякої точки, що лежить на площині.
Зауважимо, що рівняння площини є рівнянням 1-го ступеня щодо поточних координат x, yі z.
приклади.
ЗАГАЛЬНЕ РІВНЯННЯ ПЛОЩИНИ
Можна показати, що будь-яке рівняння першого ступеня щодо декартових координат x, y, zє рівнянням деякої площини. Це рівняння записується як:
Ax+By+Cz+D=0
і називається загальним рівняннямплощині, причому координати A, B, Cтут є координати нормального вектора площини.
Розглянемо окремі випадки загального рівняння. З'ясуємо, як розташовується площина щодо системи координат, якщо один або кілька коефіцієнтів рівняння перетворюються на нуль.
A – це довжина відрізка, що відсікається площиною на осі Ox. Аналогічно, можна показати, що bі c- Довжини відрізків, що відсікаються аналізованої площиною на осях Ойі Oz.
Рівнянням площини у відрізках зручно користуватися для побудови площин.