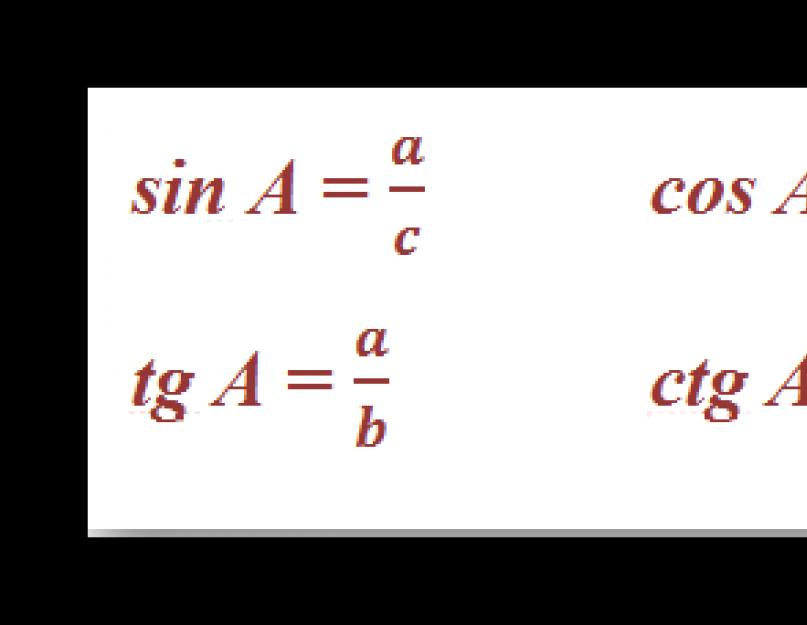Trigonometriya fan sifatida qadimgi yig'ilishda paydo bo'lgan. Birinchi trigonometrik munosabatlar astronomlar tomonidan ko'zgu orqasida aniq taqvim va yo'nalish yaratish uchun ishlab chiqilgan. Bu hisob-kitoblar sferik trigonometriyaga asoslangan edi, xuddi maktab kursi tekis trikuputning yon tomonlari va tomonlari o'rtasidagi munosabatni o'rgatadi.

Trigonometriya matematikaning trigonometrik funktsiyalarning vakolatlari va uchburchak elementlarning tomonlari va kesimlari o'rtasidagi munosabatlari bilan shug'ullanadigan bo'limidir.

Eramizning birinchi mingyilligida madaniyat va ilm-fanning rivojlanishi davrida bilimlar Qadimgi yigʻinlardan to Gretsiyagacha kengaydi. Trigonometriyaning barcha asosiy ishlanmalari Arab xalifaligi xalqining xizmatlaridir. Zokrema, turkman ta'limoti al-Marazviy asrlarda tangens va kotangens kabi funktsiyalarni bajaradi, shu jumladan sinuslar, tangenslar va kotangentlar uchun qiymatlarning birinchi jadvali. Sinus va kosinus tushunchasi hindlar tomonidan kiritilgan. Trigonometriya qadimgi Evklid, Arximed va Eratosfen kabi buyuk shaxslar tomonidan yuksak hurmatga sazovor bo'lgan.

Trigonometriyaning asosiy miqdorlari

Raqamli argumentning asosiy trigonometrik funktsiyalari sinus, kosinus, tangens va kotangensdir. Ularning har biri o'z grafigiga ega: sinus, kosinus, tangens va kotangens.

Pifagor teoremasi miqdorlarning qiymatlarini tushunish uchun formulalar uchun asosdir. Maktab o'quvchilari "Pifagor shimlari, har tomondan teng" formulasini ko'proq bilishadi, chunki isbot ekvifemoral trikutinumning dumbasiga asoslangan.

Sinus, kosinus va boshqa shartlar har qanday to'g'ri chiziqli trikutaning qirralari va tomonlari o'rtasida aloqa o'rnatadi. Keling, A kesma uchun bu miqdorlarni taqsimlash va trigonometrik funktsiyalarning oddiy o'zaro bog'lanishi formulalarini kiritamiz:

Ko'rib turganingizdek, tg va ctg - eshik funksiyalari. Agar biz a oyog'ini sin A va gipotenuza c ga qo'shimcha sifatida, b oyog'ini cos A * c deb ko'rsak, u holda tangens va kotangens uchun quyidagi formulalarni olishimiz mumkin:

Trigonometrik rang

Prognoz qilingan miqdorlarning grafik tasviri quyidagicha amalga oshirilishi mumkin:

Doira a ning barcha mumkin bo'lgan qiymatlariga ega - 0 ° dan 360 ° gacha. Chaqaloqdan ko'rinib turibdiki, terining funktsiyasi terining kattaligiga qarab salbiy yoki ijobiy qiymatga ega bo'ladi. Masalan, sin a "+" belgisi bo'ladi, chunki a qoziqning 1 va 2 choraklariga qo'yilgan, shuning uchun u 0 ° dan 180 ° gacha bo'ladi. 180 ° dan 360 ° gacha (III va IV chorak) ko'rishda sin a faqat salbiy qiymatlarga ega bo'lishi mumkin.

Keling, aniq qiymatlar uchun trigonometrik jadvallarni yaratishga harakat qilaylik va miqdorlarning qiymatlarini aniqlaymiz.

30°, 45°, 60°, 90°, 180° a darajalarining qiymatlari yaqin tomchilar deb ham ataladi. Trigonometrik funktsiyalarning qiymatlari tahlil qilinadi va maxsus jadvalda taqdim etiladi.

Bu tasvir umuman tasodifiy emas. Jadvaldagi p qiymatlari radyanlar uchun. Radiy, qoziq yoyining oxiri radiusni ko'rsatganda, bir xil bo'ladi. Boulning bu qiymati universal qiymatni o'rnatish uchun kiritilgan; radianlarda kengayish bilan, radiusning samarali ikki baravar ko'payishi, qarang.

Trigonometrik funktsiyalar uchun jadvaldagi qiymatlar radian qiymatlariga asoslanadi:

Xo'sh, 2p doiradan tashqarida yoki 360 ° ekanligini taxmin qilish muhim emas.

Trigonometrik funksiyalarning kuchi: sinus va kosinus

Sinus va kosinus, tangens va kotangensning asosiy kuchlarini ko'rib chiqish va tenglashtirish uchun ularning funktsiyalarini nomlash kerak. Buni ikki o'lchovli koordinatalar tizimidan chizilgan egri chiziqqa qarash orqali amalga oshirish mumkin.

Sinus va kosinusning kuchlar jadvaliga qarang:

Sinusoid	Kosinus
y = sinx	y = cos x
ODZ [-1; 1]	ODZ [-1; 1]
sin x = 0, x = pk uchun, bu erda k s Z	cos x = 0 da x = p/2 + pk, bu yerda k s Z
sin x = 1, x = p/2 + 2pk uchun de k s Z	cos x = 1 da x = 2pk, bu yerda k s Z
sin x = - 1 da x = 3p/2 + 2pk, de k s Z	cos x = - 1 da x = p + 2pk, de k s Z
sin (-x) = - sin x, u holda funksiya juftlashtirilmagan	cos (-x) = cos x, bu parn funksiyasi
	funksiya davriy, eng qisqa davr 2p
sin x › 0, x o‘rinda I va II choraklarda yoki 0° dan 180° gacha (2pk, p + 2pk)	cos x › 0, x da I va IV choraklarni joylashtiring yoki 270° dan 90° gacha (- p/2 + 2pk, p/2 + 2pk)
sin x ‹ 0, x III va IV choraklarda yotadi yoki 180° dan 360° gacha (p + 2p, 2p + 2p)	cos x ‹ 0, x bilan II va III choraklarda yoki 90° dan 270° gacha (p/2 + 2pk, 3p/2 + 2pk)
interval bilan o'sadi [- p/2 + 2pk, p/2 + 2k]	interval bilan o'sadi [-p + 2pk, 2pk]
[p/2 + 2pk, 3p/2 + 2pk] oraliqlari bilan o'zgaradi	intervallar orasidagi o'zgarishlar
pokhídna (sin x)’ = cos x	Pokhidna (cos x)' = - sin x

Bu bug 'xonasining vazifasi juda oddiy emasligini anglatadi. Trigonometrik miqdorlarning belgilari bilan trigonometrik doirani aniqlash va grafikni OX o'qi bo'ylab "katlama" haqida o'ylash kifoya. Agar belgilar mos kelsa, funksiya juftlashtiriladi, aks holda u ajratilmaydi.

Radianlarning kiritilishi va sinus va kosinusning asosiy kuchlarini qayta talqin qilish bizga muntazamlikni o'rnatishga imkon beradi:

Formulaning to'g'riligini o'zgartirish juda oson. Misol uchun, x = p/2 uchun sinus 1 ga teng, x = 0 ning kosinasi kabi. Tekshirish jadvalda yoki berilgan qiymatlar uchun egri funktsiyalarni bajarish orqali amalga oshirilishi mumkin.

Tangens va kotangentlarning kuchi

Tangens va kotangent funksiyalarning grafiklari sinus va kosinusdan sezilarli darajada farq qiladi. tg va ctg qiymatlari bir xil.

1. Y = tan x.
2. Tangens x = p/2 + pk da y qiymatiga teng, lekin í̈x ga etib bormaydi.
3. Tangensning eng kichik musbat davri p ga teng.
4. Tg (-x) = - tg x, u holda funksiya juftlashtirilmagan.
5. Tg x = 0 da x = pk.
6. Funktsiya o'sib bormoqda.
7. Tg x › 0, x s uchun (pk, p/2 + pk).
8. Tg x ‹ 0, x s uchun (— p/2 + pk, pk).
9. Pokhidna (tg x)' = 1/cos 2 ⁡x .

Matn ostidagi kotangentning grafik tasvirini ko'rib chiqamiz.

Asosiy quvvat kotangentlari:

1. Y = karavot x.
2. Sinus va kosinus funktsiyalarini almashtirib, tangens Y barcha haqiqiy sonlarning qiymatlarini ko'rsatishi mumkin.
3. Kotangent x = p da y ning qiymatiga teng, lekin ich ga etib bormaydi.
4. Kotangensning eng kichik musbat davri p ga teng.
5. Ctg (-x) = - ctg x, keyin funksiya juftlashtirilmagan.
6. Ctg x = 0, x = p/2 + pk uchun.
7. Funktsiya faol emas.
8. Ctg x › 0, x s uchun (pk, p/2 + pk).
9. Ctg x ‹ 0, x s uchun (p/2 + pk, pk).
10. Pokhídna (ctg x)’ = — 1/sin 2 ⁡x Vipravity

Dastlab, to'rtburchaklar trikutan to'qimalarning qiymatlarini kengaytirish zarurati tufayli sinus va kosinus ishlatilgan. Ta'kidlanganidek, to'rtburchak uchburchakli baliqlarda kesikulalarning daraja qiymati o'zgarmaydi, keyin tegishli tomonlar, hatto kun oxirida ikkala tomon ham o'zgargan bo'lsa ham, abadiy bir xillikdan mahrum bo'ladi.

Shunday qilib sinus va kosinus tushunchasi paydo bo'ldi. To'g'ri ichakning trikuputidagi o'tkir kesmaning sinusi protidal oyoqning gipotenusga, kosinus esa qo'shni oyoqning gipotenusga cho'zilishidir.

Kosinuslar va sinuslar teoremalari

Ale kosinuslari va sinuslari nafaqat to'g'ridan-to'g'ri kesilgan trikutlarda turg'un bo'lishi mumkin. To'mtoq yoki o'tkir kesishning ma'nosini bilish uchun har qanday trikutning tomoni, kosinuslar va sinuslar teoremasini aytish kifoya.

Kosinuslar teoremasi oddiy: "Uchburchak tomonining kvadrati bu tomonlarning bo'ysunishi ular orasidagi tomonning kosinusiga teng bo'lgandan keyin qolgan ikki tomonning kvadratlari yig'indisiga teng".

Sinuslar teoremasining ikkita talqini mavjud: kichik va kengaytirilgan. Bu eng kichigiga ayon: "Trikutining yon tomonlariga mutanosib bo'lgan etaklari bor." Ushbu teorema ko'pincha trikutnikda tasvirlangan qoziqning kuchini o'z ichiga olgan holda kengaytiriladi: "Trikutnikda qoziqlar proksimal tomonlarga proportsionaldir va ularning nisbati tasvirlangan qoziqning diametriga tengdir".

Pokhídni

Pokhidna - bu funktsiyani argumentini o'zgartirish orqali qanday tez o'zgartirish mumkinligini ko'rsatadigan matematik vosita. Ular fan, geometriya va bir qator texnik fanlarga qiziqishadi.

Eng muhim vazifani bajarish uchun shunga o'xshash trigonometrik funktsiyalarning jadval qiymatlarini bilish kerak: sinus va kosinus. Sinus kosinusga o'xshaydi va kosinus sinus bo'lib, minus belgisi mavjud.

Matematika bo'yicha zastosuvannya

Ayniqsa, sinuslar va kosinuslarning vikorizatsiyasi toʻgʻri chiziqli trikutlarning uchlari va ular bilan bogʻliq boʻlgan buyruqlar holida keng tarqalgan.

Sinuslar va kosinuslarning aniqligi texnologiyada o'z ifodasini topdi. Ikkala tomondan kosinuslar va sinuslar teoremalarini baholash oson edi, katlamali raqamlar va narsalarni "oddiy" uch qismga bo'lish. Ko'pincha turli tomonlar va darajadagi tuzilmalarning o'ng tomonida ishlaydigan muhandislar jadvalsiz kesmalarning kosinuslari va sinuslarini hisoblash uchun ko'p soat va kuch sarfladilar.

Keyin turli xil sinuslar, kosinuslar, tangenslar va kotangentlarning minglab qiymatlarini joylashtirish uchun Bradis jadvallari yordamga keldi. Xristianlik soatlarida omonatchilar o'z izdoshlari uchun muammo yaratdilar, Bradis stolini eslang.

Radian - teng radiusga ko'ra yoyning ekstremal qiymati yoki 57,295779513 daraja.

Daraja (geometriyada) - qoziqning 1/360 qismi yoki tekis kesmaning 1/90 qismi.

p = 3,141592653589793238462… (taxminan Pi qiymati).

Kosinus trigonometrik funktsiya, shuningdek, trigonometriyaning asosiy funktsiyalaridan biridir. To‘g‘risimon tipdagi trikutinumdagi kesik kosinusi trikutinumning qo‘shni oyog‘ining trikutinum gipotenusiga cho‘zilishidir. Ko'pincha, kosinusning qiymati trikutan tip bilan bog'liq. Ammo shunday bo'ladiki, har qanday holatda ham to'g'ridan-to'g'ri tipdagi kosinusni hisoblash kerak bo'ladi, bunda rektikutan tip kengayishlarga ega emas. Nima qilish kerak? Kuta trikutnikining kosinusini qanday bilish mumkin?

Agar siz kesmaning kosinusini to'g'ri chiziqli turdagi hisoblashingiz kerak bo'lsa, unda hamma narsa juda oddiy. Bundan tashqari, eng katta ahamiyatga ega bo'lgan kosinusning qiymatini taxmin qilish kerak. Siz faqat qo'shni oyoq orasidagi bir xil pozitsiyalarni, shuningdek, trikutanning gipotenuzini bilishingiz kerak. Rostini aytsam, bu erda kesishning kosinusini aniqlash muhim emas. Formula quyidagicha ko'rinadi: - cosa = a/c, bu erda "a" oyoqning kaptaridir va "c" tomoni gipotenuzaning kaptaridir. Masalan, to'g'ri kesmaning to'g'ri kesimining kosinusini ushbu formula yordamida topish mumkin.

Agar siz kosinusning ma'lum bir uchburchakda necha yoshda ekanligini bilmoqchi bo'lsangiz, u holda kosinus teoremasi yordamga keladi, bu shunga o'xshash vaziyatlarda tezlashtirish uchun ishlatilishi mumkin. Kosinuslar teoremasi shuni aytadiki, tricub tomonining kvadrati apriori bir xil trikubning boshqa tomonlari kvadratlari yig'indisiga teng, hatto bu tomonlar o'sha kesimning kosinusiga qo'shilmasa ham, bu farq ular orasida.

1. Trikutnik o'tkir kesishning kosinusini bilishi kerakligi sababli, uni quyidagi formuladan foydalanib hisoblash kerak: cosa = (a 2 + b 2 – c 2)/(2ab).
2. Trikutnik o'tmas kesmaning kosinusini bilishi kerakligi sababli uni quyidagi formula yordamida hisoblash kerak: cosa = (z 2 – a 2 – b 2)/(2ab). Formuladagi belgilar - a va b - kesmaga ulashgan ikki tomon uchun, c - kesmaga ulashgan tomonning yarmi uchun.

Kosinusni sinuslarning qo'shimcha teoremasi yordamida ham hisoblash mumkin. Ko'rinib turibdiki, trikubitusning yon tomonlari sajda singari kesikulalarning sinuslariga proportsionaldir. Sinuslarning qo'shimcha nazariyasidan foydalanib, trikutellum elementlarining tuzilishini, shu jumladan ikki tomonni va bir tomonga qo'shni bo'lgan vugillani yoki ikkala tomon va bir tomonni bo'ylab hisoblash mumkin. Dumbaga qarang. Ruhiy muammolar: a = 1; b = 2; c=3. "A" ning proksimal tomoni bo'lgan Kut - a bilan belgilanadi, keyin formulalar bilan birlashtirilib, biz: sosa=(b²+c²-a²)/(2*b*c)=(2²+3²- 1²)/(2* 2 *3)=(4+9-1)/12=12/12=1. Mavzu: 1.

Agar birining kosinusini trikubitul ustida hisoblash kerak bo'lsa va boshqasi juda geometrik shakl bo'lsa, unda hamma narsa biroz murakkablashadi. Kutning qiymatini birinchi navbatda radian yoki darajalarda hisoblash kerak, so'ngra bu qiymatning kosinusini hisoblash kerak. Raqamli qiymatlar uchun kosinus Bradis jadvali, muhandislik kalkulyatorlari yoki maxsus matematik dasturlar yordamida hisoblanadi.

Maxsus matematik dasturlar u yoki bu raqamning kosinuslarini avtomatik sozlash kabi funktsiyalarni bajarishi mumkin. Bunday qo'shimchalarning afzalligi shundaki, ular to'g'ri dalillarni beradi va kotib qiyin vazifalarni bajarish uchun vaqtini behuda sarflamaydi. Boshqa tomondan, muammolarni hal qilish uchun qo'shimchalardan doimiy foydalanish bilan trikutan mushaklar va boshqa yirik raqamlardagi kosinuslarni topish bo'yicha matematik muammolarni hal qilishda barcha robotik ko'nikmalar yo'qoladi.

Trigonometriya - matematikaning trigonometrik funktsiyalar va ularni amaliyotda qo'llash bilan shug'ullanadigan bo'limi. Bunday funktsiyalar hisobga olinadi sinus, kosinus, tangens va kotangens.

Sinus trigonometrik funktsiya emas, Protilaj oyog'ining kattaligining gipotenus o'lchamiga bog'liqligi

Trigonometriyada sinus.

Yuqorida aytib o'tilganidek, sinus trigonometriya va trigonometrik funktsiyalar bilan bevosita bog'liq. Uning vazifasi mo'ljallangan

• trikutnikning yon tomonlari o'lchamlari mashhurligi uchun kesishni ochishga yordam berish;
• kesishning mashhurligi sababli trikutning yon tomonining o'lchamini aniqlashga yordam beradi.

Shuni esda tutish kerakki, sinusning qiymati trikumusning har qanday o'lchami uchun har doim bir xil bo'ladi, chunki sinus o'lim emas, balki munosabatlardir.

Shuning uchun teri muammolari va boshqa muammolar uchun ushbu doimiy qiymatni o'zgartirmaslik uchun maxsus trigonometrik jadvallar yaratildi. Sinuslar, kosinuslar, tangenslar va kotangenslarning qiymatlari allaqachon qayta ishlangan va himoyalangan. Ushbu jadvallarni algebra va geometriya jadvallariga joylashtiring. Siz ularni Internetda ham topishingiz mumkin.

Geometriya sinusi.

Geometriya muhim, shuning uchun amalda tushunish uchun, sin kuta nima trikutnikni tekis kesish bilan bo'yash kerak.

To'g'ridan-to'g'ri kesishni yaratadigan tomonlar chaqirilishi qabul qilinadi a, c, protilegny em kut - X.

Zavdannya da Zazvichay dovjin tomonlarini ko'rsatdi. Qabul qilinadi a = 3, = 4. Bu safar munosabatlar ¾ ga o'xshaydi. Buni qilganingizda, trikutnikning yon tomonlarini torting, shunda ular o'tkir chetiga yotadi X, keyin oshirish va tomonlar Aі V va gipotenuza - to'g'ri ichakning tagiga to'g'ri ichak ostida yotmaydigan uchinchi tomoni. Endi trikutning tomonlarini boshqacha deb atash mumkin, aytaylik: m, n, k.

Ushbu versiyada trigonometriya qonuni qo'llaniladi: tricubening deyarli har bir tomoni o'zgargan, ammo pozitsiyasi o'zgarmagan.

Maykaning yon tomonlarini imkon qadar ko'p marta o'zgartirganda va kesishning saqlangan qiymati bilan tomonlar o'rtasidagi munosabatlar hali ham o'zgarmagan holda yo'qolishi ancha oldin qayd etilgan. Bizning holatda, ikki tomon quyidagicha o'zgarishi mumkin: a/b = ¾, qaram tomonlar bilan A 6 sm gacha, va V- 8 sm gacha sozlanishi mumkin: m/n = 6/8 = 3/4.

Ortokutan trikutaneumning yon tomonlari o'rtasidagi munosabat va tsilindr bilan aloqasi quyidagicha nomlandi:

• x kesmaning sinusi - protidal oyoqning gipotenusgacha cho'zilishi: sinx = a / c;
• x kesimning kosinasi - qo'shni oyoqning gipotenusga nisbati: cosx = h/s;
• kesmaning tangensi x - protidal oyoqning qo'shni oyoqqa cho'zilishi: tgx = a/b;
• Kesimning kotangenti x - qo'shni oyoqning protidal oyoqqa cho'zilishi: ctgx = v/a.

Trigonometriya - geometriyadagi trigonometrik funktsiyalar va ularning hosilalari bilan shug'ullanadigan matematika fanining bir tarmog'i. Trigonometriyaning rivojlanishi qadimgi Yunonistonda boshlangan. O'rta asrlar davomida Hindistonning yaqinlashishi davrida bu fanning rivojlanishiga muhim hissa qo'shildi.

Ushbu maqola trigonometriyaning asosiy tushunchalari va ma'nolariga bag'ishlangan. U asosiy trigonometrik funktsiyalarning ma'nosini ko'rib chiqadi: sinus, kosinus, tangens va kotangens. Ularning o'rni geometriya kontekstida tushuntirilgan va tasvirlangan.

Dastlab, argumenti kesilgan trigonometrik funktsiyalarning ahamiyati to'g'ridan-to'g'ri tricupusning tomonlari munosabati orqali ifodalangan.

Trigonometrik funktsiyalarning qiymatlari

Kesimning sinusi (sin a) - bu kesmadan gipotenuzaga qadar cho'zilgan yuqori tomon.

Oyoqning kosinasi (cos a) - qo'shni oyoqning gipotenusga kengayishi.

Kesimning tangensi (t g a) - protidal oyoqning qo'shni oyoqqa cho'zilishi.

Kesimning kotangensi (c t g a) - qo'shni oyoqning protidal oyoqqa cho'zilishi.

To'g'ridan-to'g'ri kesilgan trikutnikning issiq kesilishi uchun o'lpon beriladi!

Keling, tasvirlab beraylik.

To'g'ridan-to'g'ri kesilgan C bo'lgan trikutan ABCda sinus kesmasi miloddan avvalgi oyog'ining AB gipotenusu bilan qadimgi munosabatiga ega.

Sinus, kosinus, tangens va kotangens qiymatlari tricubitus tomonlarining ma'lum dovjinlari orqasida ushbu funktsiyalarning qiymatlarini hisoblash imkonini beradi.

Iltimos, esda tuting!

Sinus va kosinus qiymatlari diapazoni: -1 dan 1 gacha. Boshqacha qilib aytganda, sinus va kosinus qiymatlarni -1 dan 1 gacha oshiradi. Tangens va kotangens qiymatlari diapazoni butun son chizig'idir, shunday qilib, bu funktsiyalar har qanday qiymatlarni oshirishi mumkin.

Ma'no, haqiqatni hisobga olgan holda, o'tkir qirralarga olib boriladi. Trigonometriyada aylanish tushunchasi kiritiladi, uning kattaligi ekstremal oxirida 0 dan 90 gradusgacha bo'lgan ramkalar bilan o'ralgan emas.

Shu nuqtai nazardan, ma'lum bir kattalikdagi sinus, kosinus, tangens va kotangensning ma'nosini aniqlash mumkin. Koʻrinib turadigan yagona markaz Dekart koordinata tizimining kosasida joylashgan.

Koordinatalari (1, 0) bo'lgan A kob nuqtasi bitta qoziq markazi atrofida oxirigacha aylanadi va A 1 nuqtaga o'tadi. Qiymat A 1 (x, y) nuqtaning koordinatalari orqali beriladi.

Aylanish sinusi (gunohi).

Aylanish sinusi A 1 (x, y) nuqtaning ordinatasidir. sin a = y

Aylanishning kosinus (cos).

Aylanish kosinasi a - A 1 (x, y) nuqta abscisining ce. cos a = x

Burilishning tangensi (tg).

Burilish tangensi - A 1 (x, y) nuqta ordinatasining abssizga nisbati. t g a = y x

Aylanish kotangenti (ctg).

Aylanishning kotangensi A 1 (x, y) nuqta abssiziyasining ordinataga nisbati hisoblanadi. c t g a = x y

Har qanday burilish burchagi uchun sinus va kosinus hisoblab chiqiladi. Aylanishdan keyingi nuqtaning hatto abscis va ordinatasini ham har qanday vugil uchun hisoblash mumkinligi mantiqan to'g'ri. Aks holda tangens va kotangens bilan o'ngda. Aylanishdan keyingi nuqta nol abscissa (0, 1) va (0, - 1) nuqtaga aylantirilsa, teginish aniqlanmaydi. Bunday hollarda t g a = y x tangensi uchun farq oddiygina mantiqiy emas, qolgan qismi esa nolga tushadi. Vaziyat kotangent bilan o'xshash. Farqi shundaki, kotangens tenglamalarda aniqlanmagan, chunki nuqta ordinatasi nolga teng.

Iltimos, esda tuting!

Har qanday a kesim uchun sinus va kosinus aniqlanadi.

Barcha kesmalar uchun qiymatlar tangensi, shu jumladan a = 90 ° + 180 ° k, k ∈ Z (a = p 2 + p k, k ∈ Z)

Barcha kesimlar uchun qiymatlar kotangenti, shu jumladan a = 180 ° k, k ∈ Z (a = p k, k ∈ Z)

Aksariyat amaliy vaziyatlarda "aylanish sinusi" demang. Kontekstda va tushunarli tarzda nima sodir bo'layotgani sababli "burchakda" so'zlari shunchaki olib tashlandi.

Raqamlar

Aylanishni emas, balki sonning sinusini, kosinusini, tangensini va kotangensini qanday aniqlash mumkin?

Sonning sinus, kosinus, tangensi, kotangensi

Sonning sinus, kosinus, tangensi va kotangensi t sinus, kosinus, tangens va kotangensga o'xshash son deyiladi t radian

Masalan, sonning sinusi 10 p rad aylanish sinusiga nisbatan 10 p ga teng.

Sonning sinusini, kosinusini, tangensini va kotangensini hisoblashning yana bir usuli mavjud. Keling, uning hisobotini ko'rib chiqaylik.

Qanday samarali raqam bo'lishidan qat'iy nazar t nuqta to'g'ri burchakli Dekart koordinata tizimining kobida joylashgan bitta g'ildirak ustida joylashgan. Berilgan nuqtaning koordinatalari orqali sinus, kosinus, tangens va kotangens hisoblanadi.

Qoziqdagi kob nuqtasi koordinatalari (1, 0) bo'lgan A nuqtadir.

Ijobiy raqam t

Salbiy raqam t Nuqta kob nuqtasi kesib o'tayotganini bildiradi, go'yo siz yil o'qi qarshisidagi qoziq bo'ylab dumalab, t yo'lidan o'tasiz.

Endi raqam va nuqtaning bog'lanishi o'rnatilgan bo'lsa, sinus, kosinus, tangens va kotangens qiymatiga o'tamiz.

t ning sinusi (gunohi).

Raqamning sinusi t- songa mos keladigan bitta qoziq nuqtasining ordinatasi t. sin t = y

Kosinus (cos) t

Sonning kosinusu t- bitta qoziqning abscis nuqtasi, bu raqamni bildiradi t. cos t = x

Tangensi (tg) t

Sonning tangensi t- ordinataning soniga mos keladigan bitta qoziq nuqtasining abscisiga munosabati t. t g t = y x = sin t cos t

Qolgan ma’nolar esa tabiatga mos bo‘lib, gap boshida keltirilgan ma’noga zid kelmaydi. Raqamga mos keladigan qoziqdagi dog' t nuqtaga yuguring, so'ngra burchakka burilgandan so'ng kob nuqtasini kesib o'ting t radian

Kesimning trigonometrik funksiyalari va son argumenti

Kesimning teri qiymati kesma sinus va kosinusning turli qiymatlari bilan belgilanadi. Shuningdek, barcha a qiymatlariga kelsak, a = 90 ° + 180 ° k, k ∈ Z (a = p 2 + p k, k ∈ Z) tangens uchun boshqa qiymatni bildiradi. Yuqorida aytib o'tilganidek, barcha a uchun qiymatlarning kotangenti, shu jumladan a = 180 ° · k, k ∈ Z (a = p · k, k ∈ Z).

Aytish mumkinki, sin a, cos a, t g a, c t g a alfa funktsiyalari yoki argumentning funktsiyalari emas.

Xuddi shunday, siz sonli argumentning funktsiyalari sifatida sinus, kosinus, tangens va kotangens haqida gapirishingiz mumkin. Teri harakati raqami t sonning sinus va kosinus qiymatini ko'rsatadi t. p 2 + p · k, k ∈ Z bilan ifodalangan barcha raqamlar tangens qiymatlarini bildiradi. Xuddi shunday, kotangent barcha raqamlarga, jumladan p · k, k ∈ Z ga ham beriladi.

Trigonometriyaning asosiy funktsiyalari

Sinus, kosinus, tangens va kotangens asosiy trigonometrik funktsiyalardir.

Kontekstda trigonometrik funktsiyaning qaysi argumenti (raqamli argument yoki raqamli argument) o'ng tomonda ekanligi aniq.

Keling, kobning o'zi va 0 dan 90 darajagacha bo'lgan chegaralarda joylashgan alfa burchagi haqidagi ma'lumotlarga murojaat qilaylik. Sinus, kosinus, tangens va kotangensning trigonometrik qiymatlari to'g'ridan-to'g'ri trikutanning tomonlari o'rtasidagi munosabatlarga qo'shimcha ravishda berilgan geometrik qiymatlarga to'liq mos keladi. Keling, ko'rsataylik.

Markazi to'rtburchaklar Dekart koordinata tizimida bo'lgan yagona doirani olaylik. A(1,0) nuqtani 90 gradusgacha aylantiramiz va A1(x, y) nuqtadan abscis o‘qiga perpendikulyar o‘tkazamiz. To'g'ri kesilgan trikutda, kesilgan A 1 O H burilish a bilan bir xil, oxiri oyog'i O H, A 1 (x, y) nuqtaning abscisi. Kesim bo'ylab yotgan oyoqning dovjinasi A 1 (x, y) nuqtaning qadimgi ordinatasi, gipotenuzaning dovjinasi esa bitta qoziq radiusini qoldirib, qadimgi hisoblanadi.

Geometriyaga asoslanib, kesmaning sinusi a protilaj oyog'ining gipotenusga bo'lgan munosabatiga mos keladi.

sin a = A 1 H O A 1 = y 1 = y

Bu shuni anglatadiki, to'g'ri ichak trikuputumidagi o'tkir kesmaning bo'g'im tomoni orqali o'tadigan sinusi alfa 0 dan 90 gradusgacha bo'lgan a aylanishgacha kesilgan sinus qiymatiga ekvivalentdir.

Xuddi shunday, qiymatning mustahkamligi kosinus, tangens va kotangens uchun ko'rsatilishi mumkin.

Agar siz matnda yaxshilikni belgilagan bo'lsangiz, uni ko'ring va Ctrl+Enter tugmalarini bosing