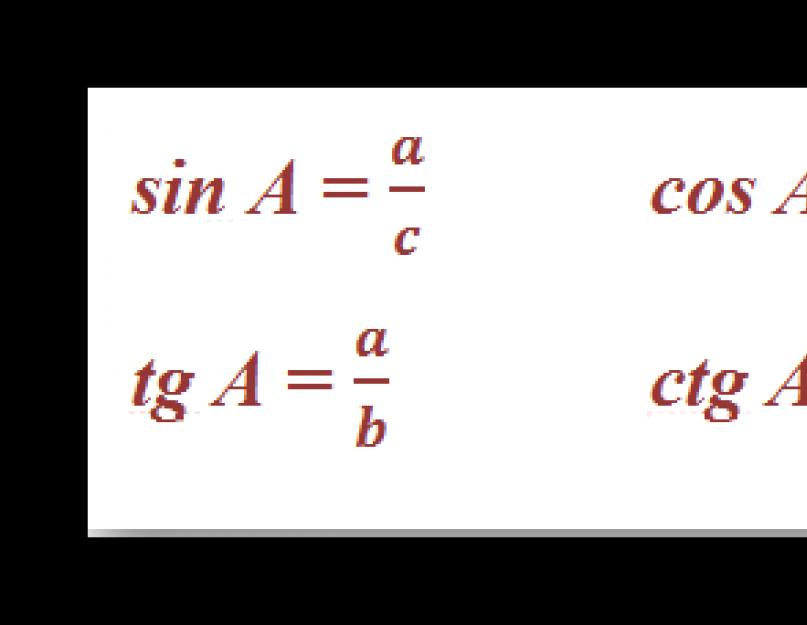ტრიგონომეტრია, როგორც მეცნიერება, წარმოიშვა უძველესი შეკრების დროს. პირველი ტრიგონომეტრიული ურთიერთობები შეიმუშავეს ასტრონომებმა, რათა შეექმნათ ზუსტი კალენდარი და ორიენტაცია სარკეების უკან. ეს გამოთვლები ეფუძნებოდა სფერულ ტრიგონომეტრიას, ისევე როგორც სასკოლო კურსი ასწავლის ბრტყელი სამკუთხედის გვერდებსა და გვერდებს შორის ურთიერთობას.

ტრიგონომეტრია არის მათემატიკის ფილიალი, რომელიც განიხილავს ტრიგონომეტრიული ფუნქციების ძალას და ტრიგონომეტრიული ელემენტების გვერდებსა და ჭრილებს შორის ურთიერთობებს.

ჩვენი ეპოქის პირველ ათასწლეულში კულტურისა და მეცნიერების განვითარების დროს ცოდნა გაფართოვდა უძველესი შეკრებიდან საბერძნეთში. ტრიგონომეტრიის ყველა ძირითადი განვითარება არაბული ხალიფატის ხალხის დამსახურებაა. ზოკრემა, ალ-მარაზვის თურქმენული სწავლებები საუკუნეებში ფუნქციონირებს როგორც ტანგენტსა და კოტანგენტს, მათ შორისაა სინუსების, ტანგენტებისა და კოტანგენტების მნიშვნელობების პირველი ცხრილი. სინუსისა და კოსინუსის ცნება შემოიღეს ინდიელებმა. ტრიგონომეტრიას დიდ პატივს სცემდნენ ძველი დროის ისეთ დიდებულ მოღვაწეებს, როგორებიც იყვნენ ევკლიდე, არქიმედე და ერატოსთენე.

ტრიგონომეტრიის ძირითადი რაოდენობები

რიცხვითი არგუმენტის ძირითადი ტრიგონომეტრიული ფუნქციებია სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი. თითოეულ მათგანს აქვს საკუთარი გრაფიკი: სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი.

პითაგორას თეორემა არის რაოდენობების მნიშვნელობების გაგების ფორმულების საფუძველი. სკოლის მოსწავლეები უფრო კარგად იცნობენ ფორმულას: „პითაგორას შარვალი, ყველა მხრიდან თანაბარი“, რადგან მტკიცებულება ეფუძნება ეკვიფემორალური ტრიკუკუტინის უკანა მხარეს.

სინუსი, კოსინუსი და სხვა პირობები ამყარებენ კავშირებს ნებისმიერი სწორხაზოვანი ტრიქტის კიდეებსა და გვერდებს შორის. მოდით შემოგთავაზოთ ფორმულები ამ რაოდენობების დაშლის A ჭრისთვის და ტრიგონომეტრიული ფუნქციების მარტივი ურთიერთდაკავშირებისთვის:

როგორც ხედავთ, tg და ctg არის კარიბჭის ფუნქციები. თუ ჩვენ ვხედავთ a ფეხს, როგორც დანამატს sin A-ს და ჰიპოტენუზას c, და ფეხს b-ს, როგორც cos A * c, მაშინ შეგვიძლია გამოვიტანოთ შემდეგი ფორმულები ტანგენტისა და კოტანგენსისთვის:

ტრიგონომეტრიული ფერი

პროგნოზირებული რაოდენობების გრაფიკული წარმოდგენა შეიძლება გაკეთდეს შემდეგნაირად:

წრეს აქვს α-ს ყველა შესაძლო მნიშვნელობა - 0°-დან 360°-მდე. როგორც ბავშვისგან ჩანს, კანის ფუნქცია კანის ზომის მიხედვით იძენს უარყოფით ან დადებით მნიშვნელობას. მაგალითად, sin α იქნება "+" ნიშანი, ვინაიდან α მოთავსებულია ფსონის 1-ლ და 2-ე მეოთხედზე, ისე, რომ ის 0°-დან 180°-მდეა. 180°-დან 360°-მდე (III და IV კვარტალი) დათვალიერებისას sin α შეიძლება ჰქონდეს მხოლოდ უარყოფითი მნიშვნელობები.

შევეცადოთ შევქმნათ ტრიგონომეტრიული ცხრილები კონკრეტული მნიშვნელობებისთვის და განვსაზღვროთ რაოდენობების მნიშვნელობები.

α დონის 30°, 45°, 60°, 90°, 180° მნიშვნელობებს ასევე უწოდებენ ახლო წვეთებს. ტრიგონომეტრიული ფუნქციების მნიშვნელობები გაანალიზებულია და წარმოდგენილია სპეციალურ ცხრილში.

ეს სურათი სულაც არ არის შემთხვევითი. ცხრილებში π მნიშვნელობები არის რადიანებისთვის. რადიუმი იგივეა, როდესაც ფსონის რკალის ბოლო მიუთითებს რადიუსზე. ბულის ეს მნიშვნელობა შემოღებულ იქნა უნივერსალური მნიშვნელობის დასამკვიდრებლად; რადიანებში გაფართოებით, რადიუსის ეფექტური გაორმაგება, იხ.

ტრიგონომეტრიული ფუნქციების ცხრილებში მნიშვნელობები ეფუძნება რადიანის მნიშვნელობებს:

ისე, არ არის მნიშვნელოვანი იმის გამოცნობა, რომ 2π არის წრის გარეთ ან 360 °.

ტრიგონომეტრიული ფუნქციების ძალა: სინუსი და კოსინუსი

სინუსის და კოსინუსის, ტანგენტისა და კოტანგენტის ძირითადი ძალების დასათვალიერებლად და გასათანაბრებლად აუცილებელია მათი ფუნქციების დასახელება. ეს შეიძლება გაკეთდეს ორგანზომილებიანი კოორდინატთა სისტემიდან შედგენილი მრუდის დათვალიერებით.

გადახედეთ სიმძლავრის ცხრილს სინუსისა და კოსინუსისთვის:

სინუსოიდი	კოსინუსი
y = sinx	y = cos x
ოძ [-1; 1]	ოძ [-1; 1]
sin x = 0, x = πk-სთვის, სადაც k ϵ Z	cos x = 0 x = π/2 + πk, სადაც k ϵ Z
sin x = 1, x = π/2 + 2πk, de k ε Z	cos x = 1 x = 2πk, სადაც k ϵ Z
sin x = - 1 x = 3π/2 + 2πk, de k ε Z	cos x = - 1 x = π + 2πk, de k ϵ Z
sin (-x) = - sin x, მაშინ ფუნქცია გაუწყვილებულია	cos (-x) = cos x, რომელიც არის parn ფუნქცია
	ფუნქცია პერიოდულია, უმოკლესი პერიოდია 2π
sin x › 0, x ადგილზე I და II კვარტალში ან 0°-დან 180°-მდე (2πk, π + 2πk)	cos x › 0, x-ზე მოათავსეთ I და IV მეოთხედები ან 270°-დან 90°-მდე (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, x-ზე მდებარეობს III და IV კვარტალზე ან 180°-დან 360°-მდე (π + 2πk, 2π + 2πk)	cos x ‹ 0, x დევს II და III კვარტალზე ან 90°-დან 270°-მდე (π/2 + 2πk, 3π/2 + 2πk)
იზრდება ინტერვალით [- π/2 + 2πk, π/2 + 2πk]	იზრდება ინტერვალით [-π + 2πk, 2πk]
იცვლება ინტერვალებით [π/2 + 2πk, 3π/2 + 2πk]	იცვლება ინტერვალებს შორის
pokhіdna (sin x)’ = cos x	ფოხიდნა (კოს x)' = - ცოდვა x

ეს ნიშნავს, რომ ორთქლის ოთახის ფუნქცია არც ისე მარტივია. საკმარისია ტრიგონომეტრიული წრის ამოცნობა ტრიგონომეტრიული სიდიდეების ნიშნებით და ვიფიქროთ გრაფიკის „დაკეცვაზე“ OX ღერძის გასწვრივ. თუ ნიშნები ემთხვევა, ფუნქცია დაწყვილდება, წინააღმდეგ შემთხვევაში ის გაუწყვილდება.

რადიანების შემოღება და სინუსისა და კოსინუსის ძირითადი ძალების ხელახალი ინტერპრეტაცია საშუალებას გვაძლევს დავადგინოთ კანონზომიერება:

ფორმულის სისწორის შეცვლა ძალიან მარტივია. მაგალითად, x = π/2-სთვის, სინუსი უდრის 1-ს, ისევე როგორც x = 0-ის კოსინუსი. შემოწმება შეიძლება გაკეთდეს ცხრილში ან მოცემული მნიშვნელობებისთვის მრუდის ფუნქციების გაშვებით.

ტანგენტებისა და კოტანგენტების ძალა

ტანგენტისა და კოტანგენტის ფუნქციების გრაფიკები მნიშვნელოვნად განსხვავდება სინუსისგან და კოსინუსისგან. tg და ctg მნიშვნელობები იდენტურია.

1. Y = tan x.
2. ტანგენსი უდრის y-ის მნიშვნელობას x = π/2 + πk-ზე, მაგრამ არ აღწევს їх-ს.
3. ტანგენსის უმცირესი დადებითი პერიოდი უდრის π.
4. Tg (-x) = - tg x, მაშინ ფუნქცია გაუწყვილებულია.
5. Tg x = 0 x = πk.
6. ფუნქცია იზრდება.
7. Tg x › 0, x ϵ-სთვის (πk, π/2 + πk).
8. Tg x ‹ 0, x ϵ-სთვის (— π/2 + πk, πk).
9. ფოხიდნა (tg x)' = 1/cos 2 ⁡x .

მოდით შევხედოთ კოტანგენტის გრაფიკულ გამოსახულებას ტექსტის ქვემოთ.

ძირითადი სიმძლავრის კოტანგენტები:

1. Y = cot x.
2. სინუსის და კოსინუსების ფუნქციების ჩანაცვლებით, ტანგენტს Y შეუძლია აჩვენოს ყველა რეალური რიცხვის მნიშვნელობა.
3. კოტანგენსი უდრის y-ის მნიშვნელობას x = πk-ზე, მაგრამ არ აღწევს ich-ს.
4. კოტანგენტის უმცირესი დადებითი პერიოდი უდრის π.
5. Ctg (-x) = - ctg x, მაშინ ფუნქცია გაუწყვილებულია.
6. Ctg x = 0, x = π/2 + πk-სთვის.
7. ფუნქცია არააქტიურია.
8. Ctg x › 0, x ϵ-სთვის (πk, π/2 + πk).
9. Ctg x ‹ 0, x ϵ-სთვის (π/2 + πk, πk).
10. Pokhіdna (ctg x)' = — 1/sin 2 ⁡x Vipraviti

თავდაპირველად, სინუსი და კოსინუსი გამოიყენებოდა მართკუთხა სამკანიანი ქსოვილების მნიშვნელობების გაფართოების აუცილებლობის გამო. აღინიშნა, რომ მართკუთხა სამკუთხა თევზში კუტების ხარისხის სამყაროს მნიშვნელობა არ იცვლება, მაშინ შესაბამისი მხარეები, თუნდაც ორივე მხარე დღის ბოლოს შეიცვალოს, სამუდამოდ მოკლებულია ერთსა და იმავეს.

ასე შემოვიდა სინუსისა და კოსინუსის ცნება. სწორი ნაწლავის ტრიკუპუტის მწვავე ჭრილობის სინუსი არის წინა ფეხის დაგრძელება ჰიპოტენუსამდე, ხოლო კოსინუსი არის მიმდებარე ფეხის გაგრძელება ჰიპოტენუსამდე.

კოსინუსების და სინუსების თეორემები

ალეს კოსინუსები და სინუსები შეიძლება სტაგნაციას განიცდიან არა მხოლოდ სწორ ჭრილში. იმისათვის, რომ იცოდეთ ბლაგვი ან მკვეთრი ჭრილის მნიშვნელობა, ნებისმიერი ტრიკუტის მხარე, საკმარისია კოსინუსების და სინუსების თეორემას ჩამოყალიბება.

კოსინუსების თეორემა მარტივია: ”სამკუთხედის გვერდის კვადრატი უდრის დანარჩენი ორი გვერდის კვადრატების ჯამს მას შემდეგ, რაც ამ გვერდების დაქვემდებარებაში ტოლია მათ შორის გვერდის კოსინუსი”.

სინუსების თეორემის ორი ინტერპრეტაცია არსებობს: მცირე და გაფართოებული. ეს აშკარაა უმცირესებისთვის: "ტრიკუტს აქვს გვერდების პროპორციული ჰემები." ეს თეორემა ხშირად ფართოვდება და მოიცავს ტრიკუტნიკში აღწერილი ფსონის ძალას: „ტრიკუტნიკში ფსონები პროქსიმალური გვერდების პროპორციულია და მათი პროპორციები უდრის აღწერილი ფსონის დიამეტრს“.

ფოხიდნი

ფოხიდნა არის მათემატიკური ინსტრუმენტი, რომელიც გვიჩვენებს, თუ როგორ შეიძლება სწრაფად შეიცვალოს ფუნქცია მისი არგუმენტის შეცვლით. ისინი დაინტერესებულნი არიან მეცნიერებით, გეომეტრიით და რიგი ტექნიკური დისციპლინებით.

ყველაზე მნიშვნელოვანი ამოცანისთვის აუცილებელია ვიცოდეთ მსგავსი ტრიგონომეტრიული ფუნქციების ცხრილის მნიშვნელობები: სინუსი და კოსინუსი. სინუსი კოსინუსის მსგავსია, ხოლო კოსინუსი არის სინუსი და არის მინუს ნიშანი.

Zastosuvannya მათემატიკაში

განსაკუთრებით ხშირია სინუსებისა და კოსინუსების ვიკორიზირება მართკუთხა ტრიქტების წვეროების და მათთან დაკავშირებული რიგის შემთხვევაში.

სინუსებისა და კოსინუსების სიცხადე ჰპოვა თავისი გამოხატულება ტექნოლოგიაში. ორივე მხრიდან ადვილი იყო კოსინუსებისა და სინუსების თეორემების შეფასება, დასაკეცი ფიგურებისა და ობიექტების დაყოფა „მარტივ“ სამ ნაწილად. ინჟინრები, რომლებიც ხშირად მუშაობენ სხვადასხვა მხარისა და ხარისხის სტრუქტურების მარჯვენა მხარეს, დახარჯეს მრავალი საათი და ძალისხმევა არატაბულური კვეთის კოსინუსებისა და სინუსების გამოთვლაში.

შემდეგ ბრედისის ცხრილები მოვიდა სამაშველოში, რათა განათავსეს სხვადასხვა ტიპის სინუსების, კოსინუსების, ტანგენტების და კოტანგენტების ათასობით მნიშვნელობა. ქრისტიანობის დროს მეანაბრეები თავიანთ მიმდევრებს უსიამოვნებას უქმნიდნენ, გაიხსენეთ ბრედის მაგიდა.

რადიანი - რკალის უკიდურესი მნიშვნელობა, თანაბარი რადიუსის მიხედვით, ანუ 57,295779513 გრადუსი.

ხარისხი (გეომეტრიაში) - ფსონის 1/360 ნაწილი ან სწორი ჭრის 1/90 ნაწილი.

π = 3.141592653589793238462… (დაახლოებით Pi-ს მნიშვნელობა).

კოსინუსი არის ტრიგონომეტრიული ფუნქცია, ისევე როგორც ტრიგონომეტრიის ერთ-ერთი მთავარი ფუნქცია. კუტუსის კოსინუსი ტრიკუკუტინუმში რექტიკუტანური ტიპის არის ტრიკუკუტინის მიმდებარე ფეხის დაგრძელება ტრიკუკუტინის ჰიპოტენუსამდე. ყველაზე ხშირად, კოსინუსის მნიშვნელობა დაკავშირებულია ტრიკუტანურ ტიპთან. მაგრამ ხდება ისე, რომ ნებისმიერ შემთხვევაში აუცილებელია კოსინუსის გამოთვლა სწორკუტანურ ტიპში, რომელშიც სწორკუტანურ ტიპს არ აქვს გაფართოებები. Რა უნდა გააკეთო? როგორ გავიგოთ კუტა ტრიკუტნიკის კოსინუსი?

თუ საჭიროა თავად ჭრილის კოსინუსის გამოთვლა სწორხაზოვანი ტიპით, მაშინ ყველაფერი ძალიან მარტივია. ასევე აუცილებელია კოსინუსის მნიშვნელობის გამოცნობა, რომელსაც უდიდესი მნიშვნელობა აქვს. თქვენ უბრალოდ უნდა იცოდეთ იგივე პოზიციები მეზობელ ფეხს შორის, ისევე როგორც ტრიკუტანური ჰიპოტენუზა. მართალი გითხრათ, აქ არ აქვს მნიშვნელობა ჭრილის კოსინუსის დადგენა. ფორმულა ასე გამოიყურება: - cosα = a/c, აქ "a" არის ფეხის მტრედი, ხოლო მხარე "c" აშკარად ჰიპოტენუზის მტრედია. მაგალითად, სწორი ჭრის კოსინუსის პოვნა შესაძლებელია ამ ფორმულის გამოყენებით.

თუ გსურთ იცოდეთ რამდენი წლისაა კოსინუსი გარკვეულ სამკუთხედში, მაშინ გვეხმარება კოსინუსების თეორემა, რომელიც შეიძლება გამოყენებულ იქნას მსგავს სიტუაციებში სიჩქარის დასაჩქარებლად. კოსინუსების თეორემა ამბობს, რომ ტრიკუბის გვერდის კვადრატი აპრიორი უდრის იმავე ტრიკუბის სხვა გვერდების კვადრატების ჯამს, თუნდაც ამ გვერდების დამატების გარეშე ამ ჭრილის კოსინუსზე, რაც განსხვავებაა. მათ შორის.

1. ვინაიდან ტრიკუტნიკმა უნდა იცოდეს მკვეთრი ჭრის კოსინუსი, მაშინ მისი გამოთვლა აუცილებელია შემდეგი ფორმულის გამოყენებით: cosα = (a 2 + b 2 – c 2)/(2ab).
2. ვინაიდან ტრიკუტნიკმა უნდა იცოდეს ბლაგვი ჭრილის კოსინუსი, აუცილებელია მისი გამოთვლა შემდეგი ფორმულის გამოყენებით: cosα = (з 2 – a 2 – b 2)/(2ab). ფორმულაში აღნიშვნებია - a და b - ორი მხარისთვის, რომლებიც კვეთს გვერდით, c - მხარის ნახევრისთვის, რომელიც მიმდებარეა ჭრილში.

კოსინუსი ასევე შეიძლება გამოითვალოს სინუსების დამატებითი თეორემის გამოყენებით. თქვენ ხედავთ, რომ ტრიკუბიტუსის გვერდები პროპორციულია კუტიკულების სინუსების, ისევე როგორც დამხობილი. სინუსების დამატებითი თეორიის გამოყენებით, შესაძლებელია გამოვთვალოთ ტრიკუტელუმის ელემენტების სტრუქტურა, მათ შორის ორი გვერდი და ვუგილა, რომელიც ერთ მხარეს არის მიმდებარე, ან ორივე მხარეს და ერთ მხარეს. შეხედე კონდახს. ფსიქიკური პრობლემები: a = 1; b = 2; c=3. Kut, რომელიც არის "A"-ს პროქსიმალური მხარე, აღინიშნება - α, შემდეგ ფორმულებთან ერთად შეგვიძლია: сosα=(b²+c²-a²)/(2*b*c)=(2²+3²- 1²)/(2*2 *3)=(4+9-1)/12=12/12=1. თემა: 1.

თუ ერთის კოსინუსი უნდა გამოითვალოს სამკუთხედზე და თუ მეორე საკმაოდ გეომეტრიული ფიგურაა, მაშინ ყველაფერი ცოტა უფრო რთული ხდება. კუტის მნიშვნელობა ჯერ უნდა გამოითვალოს რადიანებში ან გრადუსებში და შემდეგ გამოვთვალოთ ამ მნიშვნელობის კოსინუსი. რიცხვითი მნიშვნელობების კოსინუსი გამოითვლება ბრედის ცხრილის, საინჟინრო კალკულატორების ან სპეციალური მათემატიკური პროგრამების გამოყენებით.

სპეციალურ მათემატიკურ პროგრამებს შეუძლიათ შეასრულონ ფუნქციები, როგორიცაა ამა თუ იმ ფიგურის კოსინუსების ავტომატური რეგულირება. ასეთი დანამატების უპირატესობა მდგომარეობს იმაში, რომ ისინი აძლევენ სწორ მტკიცებულებებს და კლერკი არ კარგავს დროს რთულ დავალებების შესრულებაზე. მეორეს მხრივ, პრობლემების გადასაჭრელად დანამატების მუდმივი გამოყენებით, ყველა რობოტული უნარი იკარგება მათემატიკური ამოცანების გადაჭრისას კანქვეშა კუნთებში და სხვა დიდ ფიგურებში კოსინუსების პოვნაში.

ტრიგონომეტრია არის მათემატიკის ფილიალი, რომელიც ეხება ტრიგონომეტრიულ ფუნქციებს და მათ გამოყენებას პრაქტიკაში. განიხილება ასეთი ფუნქციები სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი.

სინუსი არ არის ტრიგონომეტრიული ფუნქცია, პროტილაჟის ფეხის ზომის კავშირი ჰიპოტენუსის ზომასთან

სინუსი ტრიგონომეტრიაში.

როგორც ზემოთ უკვე ითქვა, სინუსი პირდაპირ კავშირშია ტრიგონომეტრიასთან და ტრიგონომეტრიულ ფუნქციებთან. მისი ფუნქცია გამიზნულია

• ჭრის ამოხსნაში დასახმარებლად, ტრიკუტნიკის გვერდების ზომის პოპულარობისთვის;
• რათა დაეხმაროს ტრიკუტის მხარის ზომის განსაზღვრას, ჭრის პოპულარობის გამო.

უნდა გვახსოვდეს, რომ სინუსის მნიშვნელობა ყოველთვის ერთნაირია ტრიკუმუსის ნებისმიერი ზომისთვის, რადგან სინუსი არ არის სიკვდილი, არამედ ურთიერთობა.

ამიტომ, იმისათვის, რომ ეს მუდმივი მნიშვნელობა არ შეიცვალოს კანის პრობლემებისა და სხვა პრობლემებისთვის, შეიქმნა სპეციალური ტრიგონომეტრიული ცხრილები. სინუსების, კოსინუსების, ტანგენტების და კოტანგენტების მნიშვნელობები უკვე დამუშავებულია და დაცულია. მოათავსეთ ეს ცხრილები ალგებრისა და გეომეტრიის ფურცლებზე. თქვენ ასევე შეგიძლიათ იპოვოთ ისინი ინტერნეტში.

გეომეტრიის სინუსი.

გეომეტრია მნიშვნელოვანია, ამიტომ პრაქტიკაში გასაგებად, რა არის სინე კუტააუცილებელია ტრიკუტნიკის დახატვა სწორი ჭრილით.

მისაღებია, რომ მხარეები, რომლებიც ქმნიან პირდაპირ ჭრილს, ე.წ ა, გ, protilegny em kut - X.

Zazvichay at zavdannya მიუთითა dovzhin მხარეები. მისაღებია a = 3, = 4. ამჯერად ურთიერთობა ¾-ს ჰგავს. როცა ამას გააკეთებთ, ტრიკუტნიკის გვერდები ისე მოჭერით, რომ ისინი ბასრ კიდემდე დაწვნენ X, შემდეგ გაზრდა და მხარეები აі ვდა ჰიპოტენუზა არის რექტიკუტუუმის მესამე მხარე, რომელიც არ დევს სწორი ნაწლავის ქვეშ ფუძემდე. ახლა ტრიკუტის მხარეებს სხვაგვარად შეიძლება ვუწოდოთ, ვთქვათ: მ, ნ, კ.

ამ ვერსიაში გამოიყენება ტრიგონომეტრიის კანონი: ტრიკუბის თითქმის ყველა მხარე შეიცვალა, მაგრამ პოზიცია არ შეცვლილა.

ის ფაქტი, რომ მაისურის გვერდების შესაცვლელად, რაც შეიძლება ბევრჯერ და ჭრის შენახული ღირებულებით, მხარეებს შორის ურთიერთობა მაინც უცვლელი დაიკარგება, ეს დიდი ხნის წინ აღინიშნა. ჩვენს შემთხვევაში, ორმაგი მხარე შეიძლება შეიცვალოს შემდეგნაირად: a/b = ¾, დამოკიდებულ მხარეებთან ა 6 სმ-მდე და ვ- 8 სმ-მდე რეგულირება შესაძლებელია: მ/ნ = 6/8 = 3/4.

ორთოკანური ტრიკუტანუმის გვერდებს შორის ურთიერთობას და ციმთან კავშირს ეწოდა:

• x ნაჭრის სინუსი - წინამხრის ფეხის დაგრძელება ჰიპოტენუსამდე: sinx = a/c;
• x ჭრილის კოსინუსი – მიმდებარე ფეხის შეფარდება ჰიპოტენუსთან: cosx = h/s;
• ჭრილის x-ის ტანგენსი – წინამხრის ფეხის დაგრძელება მიმდებარე ფეხზე: tgx = a/b;
• ჭრის x-ის კოტანგენსი – მიმდებარე ფეხის დაგრძელება წინა ფეხზე: ctgx = v/a.

ტრიგონომეტრია არის მათემატიკური მეცნიერების ფილიალი, რომელიც ეხება ტრიგონომეტრიულ ფუნქციებს და მათ წარმოებულებს გეომეტრიაში. ტრიგონომეტრიის განვითარება ძველ საბერძნეთში დაიწყო. შუა საუკუნეების განმავლობაში მნიშვნელოვანი წვლილი შეიტანა ამ მეცნიერების განვითარებაში ინდოეთის ახლო კონვერგენციის დროს.

ეს სტატია ეძღვნება ტრიგონომეტრიის ძირითად ცნებებსა და მნიშვნელობებს. იგი უყურებს ძირითადი ტრიგონომეტრიული ფუნქციების მნიშვნელობას: სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი. მათი ადგილი ახსნილია და ილუსტრირებულია გეომეტრიის კონტექსტში.

თავდაპირველად, ტრიგონომეტრიული ფუნქციების მნიშვნელობა, რომელთა არგუმენტი ამოჭრილია, გამოიხატა სწორკუტანური ტრიკუპუსის გვერდების ურთიერთმიმართებით.

ტრიგონომეტრიული ფუნქციების მნიშვნელობები

ჭრილის სინუსი (sin α) - ზემო მხარე, რომელიც ვრცელდება ამ ჭრილიდან ჰიპოტენუზამდე.

ფეხის კოსინუსი (cos α) – მიმდებარე ფეხის დაგრძელება ჰიპოტენუსამდე.

ჭრილის ტანგენტი (t g α) - წინამხრის ფეხის დაგრძელება მეზობელზე.

ჭრილის კოტანგენსი (c t g α) - მიმდებარე ფეხის დაგრძელება წინა ფეხზე.

ხარკი ეძლევა პირდაპირ ჭრის ტრიკუტნიკის ცხელ ჭრილს!

მოდით ილუსტრირება.

ტრიკუტანურ ABC-ში C პირდაპირი ჭრილით, სინუსურ ჭრილს აქვს BC ფეხის უძველესი კავშირი AB ჰიპოტენუსთან.

სინუსის, კოსინუსის, ტანგენტისა და კოტანგენტის მნიშვნელობები საშუალებას გაძლევთ გამოთვალოთ ამ ფუნქციების მნიშვნელობები ტრიკუბიტუსის გვერდების ცნობილი დოვჟინების უკან.

Გთხოვ გახსოვდეს!

სინუსის და კოსინუსის მნიშვნელობების დიაპაზონი: -1-დან 1-მდე. სხვა სიტყვებით რომ ვთქვათ, სინუსი და კოსინუსი ზრდის მნიშვნელობებს -1-დან 1-მდე. ტანგენტისა და კოტანგენსის მნიშვნელობების დიაპაზონი არის მთელი რიცხვითი წრფე. ისე, რომ ამ ფუნქციებს შეუძლიათ გაზარდონ ნებისმიერი მნიშვნელობა.

მნიშვნელობა, ფაქტიდან გამომდინარე, მკვეთრ კიდეებამდეა გადატანილი. ტრიგონომეტრიაში შემოტანილია ბრუნვის ცნება, რომლის სიდიდე, უკიდურეს ბოლოში, არ არის გარშემორტყმული ჩარჩოებით 0-დან 90 გრადუსამდე.

ამ კონტექსტში შესაძლებელია განისაზღვროს გარკვეული სიდიდის სინუსის, კოსინუსის, ტანგენსის და კოტანგენსის მნიშვნელობა. აშკარად ერთია, რომელიც ორიენტირებულია დეკარტის კოორდინატთა სისტემის კუბზე.

Cob წერტილი A კოორდინატებით (1, 0) ბრუნავს ერთი ფსონის ცენტრის გარშემო ბოლომდე და გადადის A 1 წერტილში. მნიშვნელობა მოცემულია A 1 (x, y) წერტილის კოორდინატების მეშვეობით.

ბრუნვის სინუსი (ცოდვა).

ბრუნვის სინუსი არის A 1 (x, y) წერტილის ორდინატი. sin α = y

ბრუნვის კოსინუსი (cos).

ბრუნვის კოსინუსი α - A 1 (x, y) წერტილის აბსცისის ce. cos α = x

შემობრუნების ტანგენტი (tg).

შემობრუნების ტანგენსი არის A 1 (x, y) წერტილის ორდინატის შეფარდება აბსციზთან. t g α = y x

ბრუნვის კოტანგენსი (ctg).

ბრუნვის კოტანგენსი არის A 1 (x, y) წერტილის აბსციზის შეფარდება ორდინატთან. c t g α = x y

სინუსი და კოსინუსი გამოითვლება ბრუნვის ნებისმიერი კუთხისთვის. ლოგიკურია, რომ ბრუნვის შემდეგ წერტილის აბსცისი და ორდინატიც კი შეიძლება გამოითვალოს ნებისმიერი ვულლისთვის. წინააღმდეგ შემთხვევაში მარჯვნივ ტანგენტითა და კოტანგენტებით. ტანგენსი არ არის მითითებული, თუ წერტილი ბრუნვის შემდეგ გარდაიქმნება წერტილად, რომელსაც აქვს ნულოვანი აბსცისი (0, 1) და (0, - 1). ასეთ შემთხვევებში, t g α = y x ტანგენტის განსხვავებას უბრალოდ აზრი არ აქვს და ნაშთი ნულამდე ეცემა. ანალოგიური სიტუაციაა კოტანგენტთან დაკავშირებით. განსხვავება ისაა, რომ კოტანგენსი არ არის განსაზღვრული განტოლებებში, ვინაიდან წერტილის ორდინატი ნულის ტოლია.

Გთხოვ გახსოვდეს!

სინუსი და კოსინუსი განისაზღვრება ნებისმიერი ჭრისთვის.

მნიშვნელობების ტანგენტი ყველა ჭრილისთვის, მათ შორის α = 90 ° + 180 ° k, k ∈ Z (α = π 2 + π k, k ∈ Z)

მნიშვნელობების კოტანგენსი ყველა ჭრილისთვის, მათ შორის α = 180 ° k, k ∈ Z (α = π k, k ∈ Z)

უმეტეს პრაქტიკულ სიტუაციებში, არ თქვათ „ბრუნვის სინუსი“. სიტყვები "კუთხის გარშემო" უბრალოდ გამოტოვებულია, იმის გამო, რომ კონტექსტში და ასე გასაგებია, რა ხდება.

ნომრები

როგორ განვსაზღვროთ რიცხვის სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი და არა ბრუნვა?

რიცხვის სინუსი, კოსინუსი, ტანგენსი, კოტანგენსი

რიცხვის სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი ტეწოდება რიცხვს, რომელიც ჰგავს სინუსს, კოსინუსს, ტანგენტს და კოტანგენტს ტრადიანი

მაგალითად, რიცხვის სინუსი არის 10 π 10 π rad ბრუნვის სინუსთან შედარებით.

არსებობს კიდევ ერთი მიდგომა რიცხვის სინუსის, კოსინუსის, ტანგენსის და კოტანგენსის გამოსათვლელად. მოდით შევხედოთ მის მოხსენებას.

როგორიც არ უნდა იყოს ეფექტური რიცხვი ტწერტილი მოთავსებულია ერთ ბორბალზე, რომლის ცენტრია მართკუთხა დეკარტის კოორდინატთა სისტემის კუბიკზე. სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი გამოითვლება მოცემული წერტილის კოორდინატებით.

კობის წერტილი ფსონზე არის წერტილი A კოორდინატებით (1, 0).

დადებითი ნომერი ტ

უარყოფითი რიცხვი ტწერტილი მიუთითებს, რომ კობ წერტილი კვეთს, თითქოს წელზე ისრის მოპირდაპირე ძელზე გადადიხარ და გაივლი ბილიკს t.

ახლა, თუ რიცხვისა და წერტილის კავშირი დაყენებულია რიცხვზე, მივდივართ სინუსზე, კოსინუსზე, ტანგენტსა და კოტანგენსზე.

ტ-ის სინუსი (ცოდვა).

რიცხვის სინუსი ტ- ერთი ფსონის წერტილის ორდინატი, რომელიც შეესაბამება რიცხვს ტ. sin t = y

ტ-ის კოსინუსი (cos).

რიცხვის კოსინუსი ტ- ერთი ფსონის აბსცისის წერტილი, რომელიც მიუთითებს რიცხვზე ტ. cos t = x

ტ-ის ტანგენსი (ტგ).

რიცხვის ტანგენტი ტ- ორდინატის მიმართება ერთი ფსონის წერტილის აბსცისთან, რომელიც შეესაბამება რიცხვს ტ. t g t = y x = sin t cos t

დარჩენილი მნიშვნელობები შეესაბამება ბუნებას და არ ეწინააღმდეგება ამ პუნქტის დასაწყისში მოცემულ მნიშვნელობას. ლაქა ფსონზე, რომელიც შეესაბამება რიცხვს ტგაიქეცი წერტილისკენ და შემდეგ გადაკვეთე კობის წერტილი კუთხისკენ მიბრუნების შემდეგ ტრადიანი

ჭრის ტრიგონომეტრიული ფუნქციები და რიცხვითი არგუმენტი

ჭრილობის კანის მნიშვნელობა განისაზღვრება ჭრილის სინუსისა და კოსინუსის სხვადასხვა მნიშვნელობებით. ასევე, როგორც α ყველა მნიშვნელობისთვის, α = 90 ° + 180 ° k, k ∈ Z (α = π 2 + π k, k ∈ Z) მიუთითებს ტანგენტის განსხვავებულ მნიშვნელობაზე. კოტანგენსი, როგორც ზემოთ ითქვა, მნიშვნელობების ყველა α, მათ შორის α = 180 ° · k, k ∈ Z (α = π · k, k ∈ Z).

შეიძლება ითქვას, რომ sin α, cos α, t g α, c t g α არ არის ალფას ფუნქციები ან არგუმენტის ფუნქციები.

ანალოგიურად, შეგიძლიათ ისაუბროთ სინუსზე, კოსინუსზე, ტანგენტსა და კოტანგენსზე, როგორც რიცხვითი არგუმენტის ფუნქციები. კანის მოქმედების ნომერი ტაჩვენებს რიცხვის სინუსის და კოსინუსის მნიშვნელობას ტ. ყველა რიცხვი წარმოდგენილი π 2 + π · k, k ∈ Z მიუთითებს ტანგენტის მნიშვნელობებზე. კოტანგენსი, ანალოგიურად, ენიჭება ყველა რიცხვს, მათ შორის π · k, k ∈ Z.

ტრიგონომეტრიის ძირითადი ფუნქციები

სინუსი, კოსინუსი, ტანგენსი და კოტანგენსი არის ძირითადი ტრიგონომეტრიული ფუნქციები.

კონტექსტში ცხადია, ტრიგონომეტრიული ფუნქციის რომელი არგუმენტია (რიცხვითი არგუმენტი თუ რიცხვითი არგუმენტი) მარჯვნივ.

მოდით მივმართოთ მონაცემებს თავად კობისა და ალფა კუთხის შესახებ, რომელიც მდებარეობს 0-დან 90 გრადუსამდე საზღვრებთან. სინუსის, კოსინუსის, ტანგენსის და კოტანგენტის ტრიგონომეტრიული მნიშვნელობები სრულად შეესაბამება გეომეტრიულ მნიშვნელობებს, რომლებიც მოცემულია რექტიკუტანური ტრიკუტანის გვერდებს შორის ურთიერთობის გარდა. ვაჩვენოთ.

ავიღოთ ერთი წრე ცენტრით მართკუთხა დეკარტის კოორდინატულ სისტემაზე. მოვატრიალოთ კობ წერტილი A(1,0) 90 გრადუსამდე და A1(x, y) წერტილიდან დავხატოთ პერპენდიკულარი აბსცისის ღერძამდე. სწორხაზოვან ტრიკუტში, გაჭრა A 1 O H იგივეა, რაც α შემობრუნება, ბოლო არის ფეხი O H, A 1 წერტილის აბსციზა (x, y). ფეხის დოვჟინა, რომელიც მდებარეობს ჭრილის გასწვრივ, არის A 1 (x, y) წერტილის უძველესი ორდინატი, ხოლო ჰიპოტენუზის დოვჟინა არის უძველესი, ტოვებს ერთი ფსონის რადიუსს.

გეომეტრიიდან გამომდინარე, α ჭრილის სინუსი შეესაბამება პროტილაჟის ფეხის ურთიერთობას ჰიპოტენუსთან.

sin α = A 1 H O A 1 = y 1 = y

ეს ნიშნავს, რომ სწორი ნაწლავის ტრიკუპუტუმში სახსრის გასწვრივ მწვავე ჭრილობის სინუსის მნიშვნელობა უდრის ჭრილობის სინუსის მნიშვნელობას როტაციამდე α ალფა 0-დან 90 გრადუსამდე.

ანალოგიურად, მნიშვნელობის თანმიმდევრულობა შეიძლება ნაჩვენები იყოს კოსინუსისთვის, ტანგენსისთვის და კოტანგენსისთვის.

თუ ტექსტში მონიშნეთ უპირატესობა, გთხოვთ, ნახოთ და დააჭირეთ Ctrl+Enter