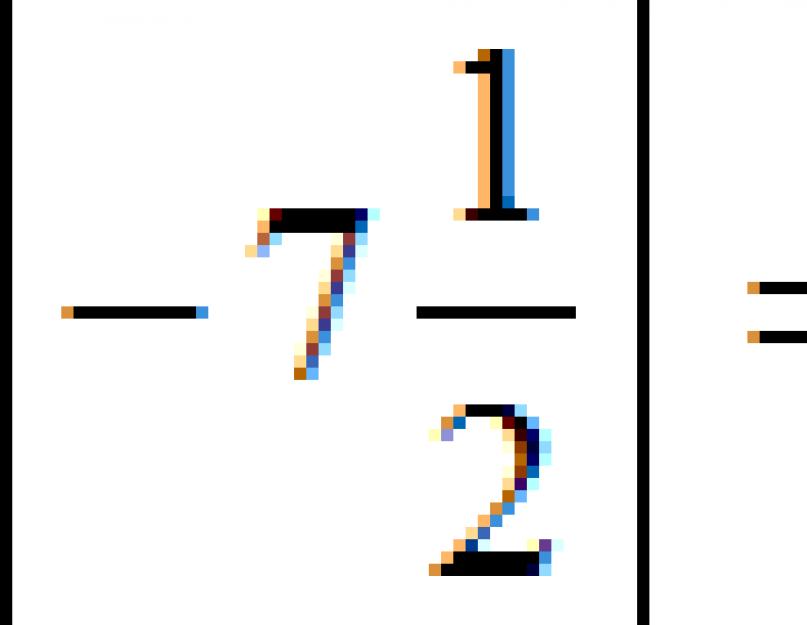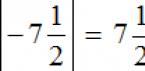Порівняння чисел - одна з найлегших і найприємніших тем з курсу математики. Втім, треба сказати, що вона не така вже й проста. Наприклад, мало хто має труднощі з порівнянням однозначних або двозначних позитивних чисел.
Але числа з великою кількістю знаків вже викликають проблеми, часто люди губляться при порівнянні негативних чисел і не пам'ятають, як порівняти два числа з різними знаками. На всі ці запитання ми й намагатимемося відповісти.
Правила щодо порівняння позитивних чисел
Почнемо з найпростішого – з чисел, перед якими не стоїть жодного знака, тобто з позитивних.
- Насамперед, варто запам'ятати, що всі позитивні числа за визначенням більші за нуль, навіть якщо йдеться про дробове число без цілого. Наприклад, десятковий дріб 0,2 буде більшим, ніж нуль, оскільки на координатній прямій відповідна їй точка все-таки віддалена від нуля на два невеликі поділки.
- Якщо йдеться про порівняння двох позитивних чисел з великою кількістю знаків, потрібно порівнювати кожен з розрядів. Наприклад - 32 і 33. Розряд десятків цих чисел однаковий, але число 33 більше, оскільки в розряді одиниць «3» більше, ніж «2».
- Як порівняти між собою два десяткові дроби? Тут потрібно дивитися перш за все на цілу частину – наприклад, дріб 3,5 буде меншим, ніж 4,6. А якщо ціла частина однакова, але чи різняться знаки після коми? У цьому випадку діє правило для цілих чисел - потрібно порівнювати знаки за розрядами доти, доки не виявляться більші і менші десяті, соті, тисячні частки. Наприклад - 4,86 більше 4,75, оскільки вісім десятих більше ніж сім.
Порівняння негативних чисел
Якщо в задачі є деякі числа –а і –с, і нам потрібно визначити, яке з них більше, то застосовується універсальне правило. Спочатку виписуються модулі цих чисел - | та |з| - і порівнюються між собою. Те число, модуль якого більше, виявиться меншим порівняно негативних чисел, і навпаки - більшим числом буде те, модуль якого менше.
Що робити, якщо порівняти потрібно негативне та позитивне число?
Тут працює лише одне правило, і воно елементарне. Позитивні числа завжди більше чисел зі знаком «мінус» - хоч би якими вони були. Наприклад, число «1» завжди буде більшим за число «-1458» просто тому, що одиниця стоїть праворуч від нуля на координатній прямій.
Також потрібно пам'ятати, що будь-яке негативне число завжди менше нуля.
Продовжуємо вивчати раціональні числа. У цьому уроці ми навчимося порівнювати їх.
З попередніх уроків ми дізналися, що чим правіше число розташовується на координатній прямій, тим більше. І відповідно, чим лівіше розташовується число на координатній прямій, тим менше.
Наприклад, якщо порівнювати числа 4 і 1, можна відразу відповісти, що 4 більше ніж 1. Це цілком логічне твердження і кожен із цим погодиться.
Як доказ можна навести координатну пряму. На ній видно, що четвірка лежить правіше за одиницю
Для цього випадку є правило, яке за бажання можна використовувати. Виглядає воно так:
З двох позитивних чисел більше число, модуль якого більше.
Щоб відповісти на запитання, яке число більше, а яке менше, спочатку потрібно знайти модулі цих чисел, порівняти ці модулі, а потім уже відповісти на запитання.
Наприклад, порівняємо ті ж числа 4 і 1, застосовуючи вищенаведене правило
Знаходимо модулі чисел:
|4| = 4
|1| = 1
Порівнюємо знайдені модулі:
4 > 1
Відповідаємо на запитання:
4 > 1
Для негативних чисел існує інше правило, виглядає воно так:
З двох негативних чисел більше те число, модуль якого менший.
Наприклад, порівняємо числа −3 та −1
Знаходимо модулі чисел
|−3| = 3
|−1| = 1
Порівнюємо знайдені модулі:
3 > 1
Відповідаємо на запитання:
−3 < −1
Не можна плутати модуль числа із самим числом. Часта помилка багатьох новачків. Наприклад, якщо модуль числа −3 більший, ніж модуль числа −1, це означає, що число −3 більше, ніж число −1.
Число −3 менше, ніж число −1 . Це можна зрозуміти, якщо скористатися координатною прямою
Видно, що число −3 лежить ліворуч, ніж −1 . А ми знаємо, що чим лівіше, тим менше.
Якщо порівнювати негативне число з позитивним, то відповідь напрошуватиметься сама. Будь-яке негативне число буде менше будь-якого позитивного числа. Наприклад, −4 менше, ніж 2
Видно, що −4 лежить ліворуч, ніж 2. А ми знаємо, що «чим лівіше, тим менше».
Тут насамперед потрібно дивитися на знаки чисел. Мінус перед числом говоритиме про те, що число є негативним. Якщо знак числа відсутній, то число є позитивним, але ви можете записати його для наочності. Нагадаємо, що це знак плюса
Ми розглянули як приклад цілі числа, виду −4, −3 −1, 2. Порівняти такі числа, а також зобразити на координатній прямій нескладно.
Набагато складніше порівнювати інші види чисел, такі як звичайні дроби, змішані числа та десяткові дроби, деякі з яких є негативними. Тут уже в основному доведеться застосовувати правила, тому що точно зобразити такі числа на координатній прямій не завжди можливо. У деяких випадках число треба буде зробити його більш простим для порівняння і сприйняття.
приклад 1.Порівняти раціональні числа
Отже, потрібно порівняти негативне число із позитивним. Будь-яке негативне число менше від будь-якого позитивного числа. Тому не гаючи часу відповідаємо, що менше, ніж
приклад 2.
Потрібно порівняти два негативні числа. З двох негативних чисел більше, модуль якого менше.
Знаходимо модулі чисел:
Порівнюємо знайдені модулі:
приклад 3.Порівняти числа 2,34 і
Потрібно порівняти позитивне число із негативним. Будь-яке позитивне число більше від будь-якого негативного числа. Тому не гаючи часу відповідаємо, що 2,34 більше, ніж
приклад 4.Порівняти раціональні числа та
Знаходимо модулі чисел:

Порівнюємо знайдені модулі. Але спочатку приведемо їх до зрозумілого вигляду, щоб простіше було порівняти, а саме переведемо в неправильні дроби та приведемо до спільного знаменника

Згідно з правилом, із двох негативних чисел більше те число, модуль якого менший. Значить раціональне більше, ніж , тому що модуль числа менший, ніж модуль числа
![]()
Приклад 5.
Потрібно порівняти нуль із негативним числом. Нуль більше будь-якого негативного числа, тому не втрачаючи часу відповідаємо, що 0 більше, ніж
Приклад 6.Порівняти раціональні числа 0 та
Потрібно порівняти нуль із позитивним числом. Нуль менше будь-якого позитивного числа, тому не втрачаючи часу відповідаємо, що 0 менше, ніж
Приклад 7. Порівняти раціональні числа 4,53 та 4,403
Потрібно порівняти два позитивні числа. З двох позитивних чисел більше число, модуль якого більше.
Зробимо в обох дробах кількість цифр після коми однаковою. Для цього в дробі 4,53 припишемо наприкінці один нуль
Знаходимо модулі чисел
Порівнюємо знайдені модулі:

Згідно з правилом, із двох позитивних чисел більше те число, модуль якого більший. Значить раціональне число 4,53 більше, ніж 4,403, тому що модуль числа 4,53 більше, ніж модуль числа 4,403
Приклад 8.Порівняти раціональні числа та
Потрібно порівняти два негативні числа. З двох негативних чисел більше те число, модуль якого менший.
Знаходимо модулі чисел:

Порівнюємо знайдені модулі. Але спочатку приведемо їх до зрозумілого вигляду, щоб простіше було порівняти, а саме переведемо змішане число в неправильний дріб, потім приведемо обидва дроби до спільного знаменника:

Згідно з правилом, із двох негативних чисел більше те число, модуль якого менший. Значить раціональне більше, ніж , тому що модуль числа менший, ніж модуль числа
Порівнювати десяткові дроби набагато простіше, ніж звичайні дроби та змішані числа. У деяких випадках, подивившись на цілу частину такого дробу, можна відразу відповісти на запитання який дріб більше, а який менше.
Щоб зробити це потрібно порівняти модулі цілих частин. Це дозволить швидко відповісти на запитання у завданні. Адже як відомо, цілі частини в десяткових дробах мають вагу більшу, ніж дробові.
Приклад 9.Порівняти раціональні числа 15,4 та 2,1256
Модуль цілої частини дробу 15,4 більший, ніж модуль цілої частини дробу 2,1256
тому і дріб 15,4 більший, ніж дріб 2,1256
15,4 > 2,1256
Іншими словами, нам не довелося витрачати час на дописування нулів дробу 15,4 і порівнювати дроби, що вийшло, як звичайні числа
154000 > 21256
Правила порівняння залишаються тими самими. У разі ми порівнювали позитивні числа.
приклад 10.Порівняти раціональні числа -15,2 і -0,152
Потрібно порівняти два негативні числа. З двох негативних чисел більше те число, модуль якого менший. Але ми порівняємо лише модулі цілих частин
Бачимо, що модуль цілої частини дробу –15,2 більший, ніж модуль цілої частини дробу –0,152.
А значить раціональне -0,152 більше, ніж -15,2 тому що модуль цілої частини числа -0,152 менше, ніж модуль цілої частини числа -15,2
−0,152 > −15,2
Приклад 11.Порівняти раціональні числа −3,4 та −3,7
Потрібно порівняти два негативні числа. З двох негативних чисел більше те число, модуль якого менший. Але ми порівняємо лише модулі цілих частин. Але проблема в тому, що модулі цілих чисел рівні:
У цьому випадку доведеться користуватися старим методом: знайти модулі раціональних чисел та порівняти ці модулі
Порівнюємо знайдені модулі:
Згідно з правилом, із двох негативних чисел більше те число, модуль якого менший. Значить раціональне −3,4 більше, ніж −3,7 тому що модуль числа −3,4 менший, ніж модуль числа −3,7
−3,4 > −3,7
приклад 12.Порівняти раціональні числа 0,(3) і
Потрібно порівняти два позитивні числа. Причому порівняти періодичний дріб із простим дробом.
Переведемо періодичний дріб 0,(3) у звичайний дріб і порівняємо його з дробом. Після переведення періодичного дробу 0,(3) у звичайний, він перетворюється на дріб
Знаходимо модулі чисел:
Порівнюємо знайдені модулі. Але спочатку приведемо їх до зрозумілого вигляду, щоб простіше було порівняти, а саме приведемо до спільного знаменника: 
Згідно з правилом, із двох позитивних чисел більше те число, модуль якого більший. Значить раціональне число більше, ніж 0,(3) тому, що модуль числа більше, ніж модуль числа 0,(3)
Сподобався урок?
Вступай у нашу нову групу Вконтакте та почні отримувати повідомлення про нові уроки
Існують певні правила порівняння чисел. Розглянемо наступний приклад.
Вчора термометр показував 15˚ C, а сьогодні показує 20˚ C. Сьогодні тепліше, ніж учора. Число 15 менше від числа 20, можемо записати так: 15< 20. А, если мы представим эти числа на координатной прямой, то точка со значением 15 будет расположена левее точки со значением 20.
Нині ж розглянемо негативні температури. Вчора на вулиці було -12˚ C, а сьогодні -8˚ C. Сьогодні тепліше, ніж учора. Тому вважають, що число -12 менше від числа -8. На горизонтальній координатній прямій точка зі значенням -12 розташована лівіше від точки зі значенням -8. Можемо записати так: -12< -8.
Отже, якщо порівнювати числа за допомогою горизонтальної координатної прямої, із двох чисел меншим вважається те, зображення якого на координатній прямій розташоване лівіше, а більшим те, зображення якого розташоване правіше. Наприклад, у нас на малюнку А > B та C, але B > C.
На координатній прямий позитивні числа розташовуються праворуч від нуля, а негативні - зліва від нуля, всяке позитивне число більше нуля, а всяке негативне менше нуля, і тому будь-яке негативне число менше всякого позитивного числа.
Отже, перше, на що необхідно звернути увагу при порівнянні чисел, – це знаки порівнюваних чисел. Число з мінусом (негативне) завжди менше позитивного.
Якщо ж ми порівнюємо два негативні числа, то потрібно порівняти їх модулі: більшим буде число, модуль якого менше, а меншим то число, модуль якого менше. Наприклад, -7 та -5. Числа, що порівнюються - негативні. Порівнюємо їх модулі 5 і 7. 7 більше ніж 5, отже -7 менше ніж -5. Якщо відзначити на координатній прямий два негативні числа, то лівіше виявиться менше число, а більше буде розташовано правіше. -7 розташовано ліворуч -5, значить -7< -5.
 Порівняння звичайних дробів
Порівняння звичайних дробів
З двох дробів з однаковими знаменниками менший той, у якого менший чисельник, і більший той, у якого більший чисельник.
Можна порівнювати дроби лише з однаковими знаменниками.
Алгоритм порівняння звичайних дробів
1) Якщо у дробу є ціла частина, порівняння починаємо саме з нього. Більшим буде той дріб, у якого ціла частина більша. Якщо цілої частини дробів немає або вони рівні, переходимо до наступного пункту.
2) Якщо дроби з різними знаменниками необхідно привести їх до спільного знаменника.
3) Порівнюємо чисельники дробів. Більшим буде той дріб, у якого чисельник більший.
Зверніть увагу, дріб із цілою частиною завжди буде більше дробу без цілої частини.
Порівняння десяткових дробів
Десяткові дроби можна порівнювати лише з однаковою кількістю цифр (знаків) праворуч від коми.
Алгоритм порівняння десяткових дробів
1) Звертаємо увагу на кількість знаків праворуч від коми. Якщо кількість цифр однакова, можемо приступати до порівняння. Якщо – ні, дописуємо потрібну кількість нулів в одному з десяткових дробів.
2) Порівнюємо десяткові дроби зліва направо: цілі з цілими, десяти з десятими, соті з сотими і т.д.
3) Більшим буде той дріб, в якому одна з частин виявиться більшою, ніж в іншому дробі (порівняння починаємо з цілих чисел: якщо ціла частина одного дробу більша, значить, і весь дріб більший).
Наприклад, порівняємо десяткові дроби:
1) Допишемо в першому дробі необхідну кількість нулів, щоб зрівняти кількість знаків після коми
57,300 та 57,321
2) Порівнювати починаємо зліва направо:
цілі з цілими: 57 = 57;
десяті з десятими: 3 = 3;
соті з сотими: 0< 2.
Оскільки соті першого десяткового дробу виявилися меншими, весь дріб і буде меншим:
57,300 < 57,321
сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.
Порівняння чисел може здійснюватися різними способами:
1) з опорою на порядок називання чисел за рахунку: число назване раніше буде меншим (це випливає з властивості упорядкованості множини натуральних чисел);
2) з опорою на процес прирахування: три і один буде чотири, отже три менше, ніж чотири;
3) з опорою на кількісні моделі порівнюваних чисел:
Для фіксації процесу порівняння запроваджується знак порівняння.
Слід пам'ятати, що порівняння - один, але читається він по-різному залежно від бажання читача. Відповідно до традиції читання текстів у європейських писемностях зліва направо перше прочитання знака порівняння зазвичай проводиться зліва направо: 3< 4 (три меньше четырех), но эту же запись при желании можно прочитать и справа налево (четыре больше трех), причем для этого не надо переставлять элементы записи таким образом: 4 >3. Не варто вселяти дитині неправильне уявлення про те, що є два знаки
порівняння, один з яких називається «менше», а інший – «більше», оскільки це формує негнучкий, конвергентний шаблон сприйняття, який потім заважатиме дитині у старшій школі під час роботи з нерівностями. Корисно пропонувати дитині кожен запис такого виду читати двома способами, наведеними вище.
7. Число 10
Десять одиниць – це десяток.
Десяток є другою лічильною одиницею в десятковій системі числення (десяткова система числення має основою число десять). Десять десятків утворюють наступну лічильну одиницю – сотню.
Число 10 є числом, що завершує перший десяток.
Число 10 є першим двозначним числом у ряді натуральних чисел.
Число 10 є першим цілим десятком, з яким знайомиться дитина.
Надалі з урахуванням поняття десяток дитина знайомиться з розрядним і десятковим складом двозначних і багатозначних чисел. Щоб не вдаватися до термінологічних складнощів і не перевантажувати матеріал раннім введенням поняття «розряд», зручно повністю провести знайомство з десятком та його записом за допомогою цифр на предметній моделі.
Знайомлячи дитину з числом 10 (першим двоцифровим числом і першим цілим десятком), дуже важливо розглянути його з різних позицій: і як нове число в ряду (наступне за дев'ятьма і тому підпорядковується загальному принципу побудови безлічі натуральних чисел), і як перше число, в записи якого використано два символи; і як нову рахункову одиницю (десяток), для чого використовують зв'язок десяти паличок як одиниця рахунку: один десяток; два десятки, три десятки...
Не слід поспішати вводити стандартні назви цих десятків (двадцять, тридцять тощо), корисніше один-два уроки використовувати зв'язки по 10 паличок для рахунку з метою формування уявлення про десяток, як лічильної одиниці.

Нуль у такій аналогії символізує зв'язку, що охоплює кільце. Для засвоєння цієї аналогії корисно відразу ж пропонувати дітям та завдання зворотного вигляду: покажіть на паличках число 30 (три зв'язки), число 40 (чотири зв'язки) тощо.
Рахунок десятками (10,20,30,40,50,60,70,80,90) - процес «технічно» аналогічний рахунку одиницями в межах 10. Корисно навчити дитину підраховувати та відраховувати десятки так само, як вона робила це з одиницями. Надалі це вміння допоможе дитині легше освоїти обчислювальні прийоми додавання та віднімання в межах 100.
При знайомстві дитини з нумерацією однозначних чисел рекомендуємо педагогу використовувати такі види завдань:
1) на спосіб утворення кожного наступного числа шляхом прирахування одиниці до попереднього:
Як із числа 3 отримати 4? (Додати до трьох один.)
2) визначення місця числа у ряду:
За яким числом стоїть число 5? (За числом 4). Де місце числа 8? (Між числами 7 і 9.)
3) порівняння як двох сусідніх, і несусідних чисел:
Порівняйте числа: 5...4 7.„2
4) до складу числа:
5) на запам'ятовування зворотної послідовності числівників у ряду: