5.1 Завдання площини
Площина задається трьома довільними точками, що не належать до однієї прямої. Площина у просторі можна задати:
· трьома точками, що не лежать на одній прямій (рисунок 5.1, а);
· Прямою і не належить їй точкою (рисунок 5.1, б);
· двома прямими, що перетинаються (рисунок 5.1, в);
· Двома паралельними прямими (рисунок 5.1, г);
· будь-якою плоскою фігурою (рисунок 5.1, д).
Малюнок 5.1
Кожен із перерахованих способів завдання площини допускає перехід до будь-якого іншого, т.к. положення прямої в площині визначається двома її точками або однією точкою та напрямом цієї прямої.
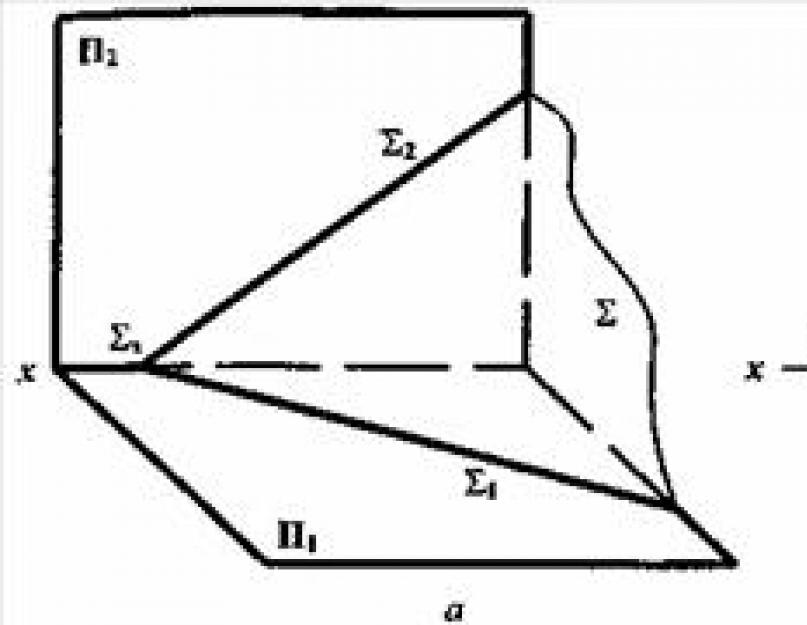
Часто застосовується спосіб завдання площини за допомогою прямих ліній (взаємно перетинаються або паралельних), якими дана площина перетинається з площинами проекцій П 1 П 2 , П 3 . Крім цього - це завдання площини слідами, у своїй зберігається наочність зображення (рисунок 5.2).

Малюнок 5.2
5.2 Сліди площини.
Лінія перетину площини з площиною проекцій (П 1 , П 2 , П 3 ) називається слідом площини. Інакше кажучи, слід площині - це пряма, що у площині проекцій. Сліду присвоюється найменування тієї поверхні проекцій, якій він належить. Наприклад, горизонтальний слід отриманий при перетині заданої площини з площиною П 1 і позначається фронтальний - з площиною П 2 (), профільний – з площиною П 3 (). Два сліди однієї й тієї ж площині перетинаються на осі проекції в точці, яка називається точкою сходу слідів. Кожен із слідів площини збігається зі своєю однойменною проекцією, решта проекцій виявляється лежачими на осях. Наприклад, горизонтальний слід площини Σ(рисунок 5.2) збігається зі своєю горизонтальною проекцією, фронтальна його проекція знаходиться на осі х, а профільна на осі у.За розташуванням слідів площини можна будувати висновки про положенні даної площини у просторі щодо площин проекцій П 1 ,П 2 , П 3 .
5.3 Положення площини щодо площин проекцій
Будь-яка, довільно взята у просторі площина, може займати загальне чи приватне становище. Площиною загального становищаназивається площина, яка не перпендикулярна до жодної з площин проекцій (див. малюнок 5.2). Всі інші площини (крім площин проекцій) відносяться до площин приватного положення і поділяються на площини, що проеціюють, і площини рівня. |Проецирующей називається площину, перпендикулярна однієї
із площин проекцій. Наприклад, горизонтально-проецуюча площина перпендикулярна до горизонтальної площини проекції П 1 (рисунок 5.3).

Малюнок 5.3
Горизонтальні проекції всіх геометричних образів (крапок, прямих, фігур), що у цій площині, збігаються з горизонтальним слідом 1 . Кут, який утворюється між площинами і П 2 проектується на П 1 без спотворення. Фронтальний слід 2 перпендикулярний до осі x.
Фронтально-проецуюча площина () перпендикулярна до фронтальної площини П 2 показана малюнку 5.4. Фронтальні проекції всіх геометричних образів (крапок, прямих, фігур), що у цій площині, збігаються з фронтальним слідом площини 2 . Кут , який утворюється між заданою площиною і П 1 проектується на П 2 без спотворення. Горизонтальний слід площини 1 перпендикулярний до осі x.

Малюнок 5.4
Профільно-проецуюча площина Т (T 1 , T 2) перпендикулярна до профільної площини проекції П 3 (рисунок 5.5).

Малюнок 5.5
Профільні проекції всіх геометричних образів (крапок, прямих, фігур), що лежать у цій площині, збігаються з профільним слідом площини Т 3 . Кути та , які утворюються між заданою площиною та площинами проекцій П 1 і П 2 (= T^П 1 ; = Т^П 2 ), проектуються на площину П3 без спотворень. Горизонтальний та фронтальний сліди площини паралельні осі х.
Профільно-проецуюча площина може проходити через вісь x: (рисунок 5.6).

Малюнок 5.6
Сліди цієї площини 1 = 2 збігаються один з одним і з віссю x тому не визначають положення площини. Необхідно, крім слідів, задати в площині крапку (рисунок 5.6). В окремому випадку ця площина може бути бісекторною площиною. Кут ° = °, а точка А рівновіддалена від площин проекцій П 1 і П 2 . Площиною рівня називається площина, перпендикулярна одночасно до двох площин проекцій і паралельна до третьої. Таких площин три різновиди (рисунок 5.7):
· горизонтальна площина рівня перпендикулярна до П 2 П 3 і паралельна П 1 (Рисунок 5.7, а);
· фронтальна площина рівня перпендикулярна до П 1 П 3 і паралельна П 2 (рисунок 5.7, б);
· Профільна площина рівня перпендикулярна до П 1 П 2 і паралельна П 3 (рисунок 5.7 в).

Малюнок 5.7
З визначення площин рівня випливає, що одна з проекцій точки, лінії, фігури, що належать цим площинам, співпадатиме з однойменним слідом площини рівня, а інша проекція буде натуральною величиною цих геометричних образів.
5.4 Ознаки приналежності точки та прямої площини
Для визначення належності точки та прямої площини, розташованої у просторі, слід керуватися такими положеннями:
· Точка належить площині, якщо через неї можна провести лінію, що лежить у площині;
· Пряма належить площині, якщо вона має з площиною хоча б дві загальні точки;
· Пряма належить площині, якщо вона проходить через точку даної площини паралельно прямий, що належить цій площині.
Через одну точку на площині можна провести безліч ліній. Це можуть бути довільні лінії та лінії, що займають особливе положення по відношенню до площин проекцій П 1 П 2 , П 3 . Пряма, що належить площині, що розглядається, проведена паралельно горизонтальній площині проекцій, називається г оризонталлюплощині.
Пряма, що належить площині, що розглядається, проведена паралельно фронтальної площини проекцій, називається фронталлюплощині.
Горизонталь та фронталь є лініями рівня.
Горизонталь поверхні слід починати будувати з передньої проекції, т.к. вона паралельна осі xгоризонтальна проекція горизонталі паралельна горизонтальному сліду площині.
Оскільки всі горизонталі площини паралельні між собою, можна вважати горизонтальний слід площини нульовою горизонталлю (рисунок 5.8).
Фронталь поверхні слід починати будувати з горизонтальної проекції, т.к. вона паралельна осі x, фронтальна проекція фронталі паралельна фронтальному сліду. Фронтальний слід площини – нульова фронталь. Усі фронталі площини паралельні між собою (рисунок 5.9).

Малюнок 5.8

Малюнок 5.9
До лінії рівня відноситься і профільна пряма, що лежить у заданій площині та паралельна П 3 .
До головних ліній особливого становищау площині, крім лінії рівня, відносяться лінії найбільшого нахилу площини до площини проекцій.
5.5 Визначення кута нахилу площини до площин проекцій
Площина загального положення, розташована в довільному просторі, нахилена до площин проекцій. Для визначення величини двогранного кута нахилу заданої площини до будь-якої площини проекції використовуються лінії найбільшого нахилу площини до площини проекцій: П 1 - лінія ската, до П 2 - лінія найбільшого нахилу площини до площини П 2 .
Лінії найбільшого нахилу площини - це прямі, що утворюють із площиною проекцій найбільший кут, проводяться в площині перпендикулярно до відповідної лінії рівня. Лінії найбільшого нахилу та її відповідна проекція утворюють лінійний кут, яким вимірюється величина двогранного кута, складеного даною площиною та площиною проекцій (рисунок 5.10).

Тепер ми перерахуємо основні методи завдання конкретної площині у просторі.
По-перше, площину можна задати, зафіксувавши три простори, що не лежать на одній прямій точці. Цей спосіб заснований на аксіомі: через будь-які три точки, що не лежать на одній прямій, проходить єдина площина.
Якщо в тривимірному просторі зафіксована прямокутна система координат і задана площина за допомогою вказівки координат трьох її різних точок, що не лежать на одній прямій, то ми можемо написати рівняння площини через три задані точки.
Два наступні способи завдання площини є наслідком попереднього. Вони засновані на слідствах з аксіоми про площину через три точки:
· Через пряму і не лежачу на ній точку проходить площину, причому тільки одна (дивіться також статтю рівняння площини, що проходить через пряму та точку);
· Через дві прямі, що перетинаються, проходить єдина площина (рекомендуємо ознайомитися з матеріалом статті рівняння площини, що проходить через дві прямі, що перетинаються).


Четвертий спосіб завдання площини у просторі ґрунтується на визначенні паралельних прямих. Нагадаємо, що дві прямі у просторі називаються паралельними, якщо вони лежать в одній площині та не перетинаються. Таким чином, вказавши дві паралельні прямі у просторі, ми визначимо єдину площину, у якій ці прямі лежать.
Якщо тривимірному просторі щодо прямокутної системи координат задана площину зазначеним способом, ми можемо скласти рівняння площині, що проходить через дві паралельні прямі.

Ознака паралельності двох площин дає нам ще один спосіб завдання площини. Згадаймо формулювання цієї ознаки: якщо дві прямі однієї площини, що перетинаються, відповідно паралельні двом прямим інший площині, то такі площини паралельні. Отже, ми можемо задати конкретну площину, якщо вкажемо точку, якою вона проходить і площину, якою вона паралельна.
В курсі середньої школипід час уроків геометрії доводиться така теорема: через фіксовану точку простору проходить єдина площина, перпендикулярна до цієї прямої. Таким чином, ми можемо задати площину, якщо вкажемо точку, через яку вона проходить, та пряму, перпендикулярну до неї.
Якщо в тривимірному просторі зафіксована прямокутна система координат і задана площина вказаним способом, то можна скласти рівняння площини, що проходить через задану точку перпендикулярно заданій прямій.
Замість прямої, перпендикулярної до площини, можна вказати один із нормальних векторів цієї площини. І тут є можливість написати загальне рівняння площини.
Ви також можете знайти цікаву інформацію в науковому пошуковику Otvety.Online. Скористайтеся формою пошуку:
Ще за темою Способи завдання площини.
- 13. Розлади мислення: за темпом, строєм, цілеспрямованістю. Діагностичне значення симптомів.
- Основні напрями у дослідженні порушень мислення при шизофренії.
- Класифікація порушень мислення на роботах Б.В. Зейгарник.
- 8. Аналіз специфіки методів спеціальної психології проти методами інших галузей психології: використання стандартизованих технік (тестів), використання анкетування, методу аналізу продуктів діяльності.
- 14. Методика вивчення площі геометричних фігур та формування навичок її вимірювання. Ознайомлення з одиницями виміру площі та їх співвідношенням. Особливості сприйняття молодшого школяра. Облік закономірностей та принципів виховання щодо площі геометричних фігур.
Площина - це одна з найбільш важливих фігур у планіметрії, тому потрібно добре розуміти, що вона являє собою. У рамках цього матеріалу ми сформулюємо саме поняття площини, покажемо, як її позначають на листі, та введемо необхідні позначення. Потім ми розглянемо це поняття в порівнянні з точкою, прямою або іншою площиною і розберемо їх варіанти взаємного розташування. Усі визначення будуть проілюстровані графічно, а потрібні аксіоми сформульовані окремо. В останньому пункті ми вкажемо, як правильно задати площину у просторі кількома способами.
Yandex.RTB R-A-339285-1
Площина є однією з найпростіших фігур у геометрії нарівні з прямою і точкою. Раніше ми вже пояснювали, що точка та пряма розміщуються на площині. Якщо цю площину розмістити у тривимірному просторі, ми отримаємо точки і прямі у просторі.
У житті уявлення про те, що таке площину, нам можуть дати такі об'єкти, як поверхня підлоги, столу чи стіни. Але треба враховувати, що у житті їх розміри обмежені, а тут поняття площини пов'язане з нескінченністю.
Прямі та точки, розміщені в просторі, ми будемо позначати аналогічно розміщеним на площині – за допомогою малих та великих латинських літер (B , A , d , q та ін.) Якщо в умовах завдання у нас є дві точки, які розташовані на прямій, то можна вибрати такі позначення, які відповідатимуть один одному, наприклад, пряма D B та точки D та B .
Щоб позначити площину на письмі, традиційно використовуються маленькі грецькі літери, наприклад, α, γ або π.
Якщо нам потрібне графічне відображення площини, зазвичай для цього використовується замкнутий простір довільної форми або паралелограм.
Площину прийнято розглядати разом із прямими, точками, іншими площинами. Завдання з цим поняттям зазвичай містять деякі варіанти їхнього розташування один щодо одного. Розглянемо окремі випадки.
Перший спосіб взаємного розташування у тому, що точка розташована площині, тобто. належить їй. Можна сформулювати аксіому:
Визначення 1
У будь-якій площині є точки.
Такий варіант розташування називається проходженням площини через точку. Щоб позначити це на листі, використовується символ ∈ . Так, якщо нам потрібно записати в буквеному вигляді, що через точку A проходить якась площина π, то ми пишемо: A ∈ π.
Якщо певна площина задана у просторі, то точок, що належать їй, є нескінченним. А якої мінімальної кількості точок буде достатньо для визначення площини? Відповіддю це питання буде наступна аксіома.
Визначення 2
Через три точки, що не розташовані на одній прямій, проходить єдина площина.
Знаючи це правило, можна запровадити нове позначення площини. Замість маленької грецької літери ми можемо використовувати назви точок, що у ній, наприклад, площину АВС.
Інший спосіб взаємного розташування точки та площини можна виразити за допомогою третьої аксіоми:
Визначення 3
Можна виділити щонайменше 4 точки, які не будуть перебувати в одній площині.
Вище ми вже зазначали, що для позначення площини у просторі буде достатньо трьох точок, а четверта може бути як у ній, так і поза нею. Якщо потрібно позначити відсутність належності точки до заданої площини на письмі, використовується знак ∉ . Запис виду A ∉ π правильно читається як «точка A не належить площині π»
Графічно останню аксіому можна так:

Найпростіший варіант – пряма знаходиться у площині. Тоді в ній будуть розташовані щонайменше дві точки цієї прямої. Сформулюємо аксіому:
Визначення 4
Якщо хоча б дві точки заданої прямої знаходяться в деякій площині, це означає, що всі точки цієї прямої розташовані в даній площині.
Щоб записати належну пряму деяку площину, використовуємо той самий символ, що й для точки. Якщо ми напишемо « a ∈ π », то це означатиме, що ми маємо пряму a , яка розташована в площині π . Зобразимо це малюнку:

Другий варіант взаємного розташування – це коли пряма перетинає площину. У такому разі у них буде лише одна загальна точка – точка перетину. Для запису такого розташування у літерному вигляді використовуємо символ ∩. Наприклад, вираз a ∩ π = M читається як «пряма a перетинає площину π у певній точці M». Якщо у нас є точка перетину, значить, у нас є кут, під яким пряма перетинає площину.
Графічно цей варіант розташування виглядає так:

Якщо ми маємо дві прямі, одна з яких лежить у площині, а інша її перетинає, то вони є перпендикулярними один одному. На листі це означає символ ⊥ . Особливості такої позиції ми розглянемо окремою статтею. На малюнку це розташування виглядатиме так:

Якщо ми вирішуємо завдання, в якому є площина, нам необхідно знати, що являє собою нормальний вектор площини.
Визначення 5
Нормальний вектор площини – це такий вектор, який лежить на перпендикулярній до прямої по відношенню до площини і не дорівнює при цьому нулю.
Приклади нормальних векторів площини показані на малюнку:

Третій випадок взаємного розташування прямої та площини – це їхня паралельність. У такому разі жодної спільної точки вони не мають. Для зазначення таких відносин на листі використовується символ. Якщо у нас є запис виду a ? Докладніше цей випадок ми розберемо у статті про паралельні площини та прямі.

Якщо пряма розташована всередині площини, вона ділить її на дві рівні або нерівні частини (напівплощини). Тоді така пряма називатиметься межею напівплощин.
Будь-які 2 точки, розташовані в одній напівплощині, лежать по одну сторону від кордону, а дві точки, що належать різним напівплощинам, лежать по різний біквід кордону.
1. Найбільш простий варіант – дві площини збігаються одна з одною. Тоді вони матимуть щонайменше три спільні точки.
2. Одна площина може перетинати іншу. У цьому утворюється пряма. Виведемо аксіому:
Визначення 6
Якщо дві площини перетинаються, між ними утворюється загальна пряма, де лежать всі можливі точки перетину.
На графіку це виглядатиме так:

У разі між площинами утворюється кут. Якщо він дорівнюватиме 90 градусам, то площини будуть перпендикулярні один одному.
3. Дві площини можуть бути паралельними другдругові, тобто не мати жодної точки перетину.

Якщо у нас є не дві, а три і більше площин, що перетинаються, то таку комбінацію прийнято називати пучком або зв'язкою площин. Докладніше про це ми напишемо в окремому матеріалі.
У цьому пункті ми подивимося, які методи завдання площині в просторі.
1. Перший спосіб заснований на одній з аксіом: єдина площина проходить через 3 точки, що не лежать на одній прямій. Отже, ми можемо задати площину, просто вказавши три такі точки.
Якщо у нас є прямокутна система координат у тривимірному просторі, в якій задана площина за допомогою цього способу, ми можемо скласти рівняння цієї площини (докладніше див, відповідну статтю). Зобразимо цей спосіб малюнку:

2. Другий спосіб – завдання площини за допомогою прямої та точки, що не лежить на цій прямій. Це випливає з аксіоми про площину через 3 точки. рисунок:

3. Третій спосіб полягає в завданні площини, яка проходить через дві прямі, що перетинаються (як ми пам'ятаємо, в такому випадку теж є тільки одна площина.) Проілюструємо спосіб так:

4. Четвертий спосіб заснований на паралельних прямих. Згадаймо, які прямі називаються паралельними: вони повинні лежати в одній площині і не мати жодної точки перетину. Виходить, що якщо ми вкажемо в просторі дві такі прямі, то тим самим зможемо визначити для них ту саму єдину площину. Якщо у нас є прямокутна система координат у просторі, в якій вже задана площина у такий спосіб, то ми можемо вивести рівняння такої площини.
На малюнку цей спосіб виглядатиме так:

Якщо ми згадаємо, що таке ознака паралельності, то зможемо вивести ще один спосіб завдання площини:
Визначення 7
Якщо у нас є дві прямі, що перетинаються, які лежать у деякій площині, які паралельні двом прямим в іншій площині, то і самі ці площини будуть паралельні.
Таким чином, якщо ми поставимо точку, то зможемо задати площину, яка проходить через неї, і ту площину, якою вона буде паралельна. У такому разі ми також можемо вивести рівняння площини (про це ми маємо окремий матеріал).

Згадаймо одну теорему, вивчену в рамках курсу геометрії:
Визначення 8
Через певну точку простору може проходити лише одна площина, яка буде паралельна заданій прямій.
Це означає, що можна задати площину шляхом вказівки конкретної точки, через яку вона проходитиме, і пряма, яка буде перпендикулярна до неї. Якщо площина задана у прямокутній системі координат, то ми можемо скласти рівняння площини для неї.

Також ми можемо вказати не пряму, а звичайний вектор площини. Тоді можна буде сформулювати загальне рівняння.

Ми розглянули основні способи, за допомогою яких можна поставити площину у просторі.
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter
Тут із прийнятих нами аксіом стереометрії ми отримаємо важливі теореми та наслідки про прямі та площини. Самі собою вони досить очевидні. Розглянемо їх докази, які показують, як будь-яке твердження можна вивести з аксіом з усіма необхідними посиланнями.
2.1 Завдання прямої двома точками
Доведення. У п. 1.1 вже доведено, що через кожні дві точки А, проходить пряма а.
Доведемо, що ця пряма лише одна. Пряма а лежить у певній площині а. Припустимо, що, крім прямої а через точки А, В проходить ще пряма b (рис. 31). По аксіомі 3 пряма, що має з площиною дві загальні точки, лежить у цій площині. Оскільки пряма b має загальні точки А і B, то b лежить у площині α.
Мал. 31
Але у площині а виконується планіметрія, отже, через дві точки А і В проходить лише одна пряма. Значить, прямі і b збігаються. Таким чином, через точки А та В проходить тільки одна пряма.
Слідство. У просторі (як і площині) дві різні прямі що неспроможні мати більше однієї загальної точки.
Дві прямі, що мають єдину загальну точку, називаються такими, що перетинаються.
Зауваження. Не завжди пропозиція, справедлива в планіметрії, вірна і в стереометрії. Так, наприклад, у площині через дві дані точки N, S проходить лише одне коло з діаметром NS, а в просторі таких кіл нескінченна безліч - у кожній площині, що проходить через точки N, S, лежить таке коло (рис. 32, а) .

Мал. 32
Але пряма, яка проходить через точки N, S у просторі, лише одна. Ця загальна пряма всіх площин, що проходять через точки N, S (рис. 32, б).
Довівши, що у просторі через кожні дві точки проходить єдина пряма, ми можемо задавати пряму у просторі будь-який парою її точок, не переймаючись у тому, як і площині ця пряма лежить. Пряма, що проходить через точки А, В, позначається (АВ).
Аналогічне вірно і для відрізків: кожні дві точки в просторі є кінцями єдиного відрізка.
2.2 Завдання площини трьома точками
Доведення. Нехай точки А, В, С не лежать на одній прямій. По аксіомі площини через ці точки проходить деяка площина (див. рис. 6). Доведемо, що вона лише одна.
Припустимо, що через точки А, B, С проходить ще одна площина (3, відмінна від а. Площини а і р мають спільні точки (наприклад, точку А). За аксіомою 2 перетином площин α і β є їх спільна пряма. На цій прямий лежать усі загальні точки площин α і β, отже, точки A, B, З. Але це суперечить умові теореми, оскільки відповідно до нього A, B, З лежать однією прямий. проходить лише одна площина?
Площина, що проходить через три точки А, В, С, що не лежать на одній прямій, позначають (ABC).
Легко проілюструвати теорему 2. Наприклад, положення дверей фіксується двома петлями і замком.
2.3 Завдання площини прямою та точкою та двома прямими
Доведення. Нехай дані пряма а і точка А, що не лежить на ній. Візьмемо на прямій а дві точки B і С (рис. 33). Точка А не лежить з ними на одній прямій, тому що через точки B та С проходить лише одна пряма - це пряма а, а точка А не лежить на ній за умовою теореми.

Мал. 33
Через точки А, B, З, що не лежать на одній прямій, проходить (за теоремою 2) єдина площина АВС. Пряма а має із нею дві загальні точки B і З і, отже, по аксіомі 3 лежить у ній. Таким чином, площина АВС і є площина, що проходить через пряму а і точку А.
Єдиність такої площини доведемо способом протилежного.
Нехай є ще одна площина, що містить пряму а і точку А. Тоді вона містить точки B і С. За теоремою 2 вона повинна збігатися з площиною АВС. Отримана суперечність і доводить єдиність.
Ось ілюстрація цієї теореми: повертаючи обкладинку книги, ви в кожний момент пальцями фіксуєте її положення.
Доведення. Нехай прямі а та b перетинаються у точці А. Візьмемо на прямій b іншу точку B (рис. 34). По теоремі 3 через пряму а і точку проходить площину а. Згідно з аксіомою 3 пряма Ь лежить у цій площині, оскільки має з нею дві загальні точки А і В. Отже, площина проходить через прямі а і b. Єдиність такої площини доведіть самостійно способом протилежного.

Мал. 34
Тепер ми знаємо три способи завдання площини:
- трьома точками, що не лежать на одній прямій;
- прямою і не лежачою на ній точкою;
- двома прямими, що перетинаються.
Запитання для самоконтролю
- Які ви знаєте способи завдання прямої у просторі?
- Які знаєте способи завдання площині?
Будь-яка геометрична фігура, занурена в простір, складається з деякої множини точок простору. Площина як одна з геометричних фігур, є сукупністю безлічі точок. З цього визначення площини можна встановити способи завдання її положення у просторі. Для цього досить згадати аксіому поєднання – через три точки, що не лежать на одній прямій, можна провести площину і лише одну.
На рис. 21 представлені способи завдання положення площини у просторі:
а – трьома точками, що не лежать на одній прямій;
б - прямий і точкою, взятої поза прямою;
в – двома прямими, що перетинаються;
г – двома паралельними прямими.
На комплексному кресленні (рис. 22) площина може бути задана:
а – проекціями трьох точок, що не лежать на одній прямій;
б – проекціями прямої та точки, взятої поза прямою;
в – проекціями двох прямих, що перетинаються;
г – проекціями двох паралельних прямих.
Кожен із представлених на рис. 22 способів завдання площини на кресленні може бути перетворено з одного в інший. Так, наприклад, провівши через точки А і (рис. 22, а) пряму, отримують завдання площини, представлене на рис. 22, б. Від нього можна перейти до способу, представленого на рис. 22 г якщо через точку С провести пряму, паралельну прямий АВ. Якщо точки А, В і С з'єднати попарно прямими, то одержують трикутник АВС – плоску фігуру (рис. 23), проекціями якої може бути задана площина на кресленні.

 При цьому завжди слід пам'ятати про те, що площина, як геометрична фігура, безмежна і тому не можна обмежуватися побудовами тільки в межах площі цього трикутника, так як у загальному випадку площини проекції займають всю кожну з площин проекцій: горизонтальну П I , фронтальну П 2 і профільну П 3 .
При цьому завжди слід пам'ятати про те, що площина, як геометрична фігура, безмежна і тому не можна обмежуватися побудовами тільки в межах площі цього трикутника, так як у загальному випадку площини проекції займають всю кожну з площин проекцій: горизонтальну П I , фронтальну П 2 і профільну П 3 .
Більш наочно площина може бути задана за допомогою прямих, якими вона перетинає площини проекцій (рис. 24, а).
Ці прямі називаються слідами площини. У загальному випадку обидва сліди повинні перетинатися між собою в точці на осі проекцій, яку називають точкою сходу слідів.
 З усього різноманіття положень площини щодо заданої системи площин проекцій зазвичай виділяють такі коли.
З усього різноманіття положень площини щодо заданої системи площин проекцій зазвичай виділяють такі коли.